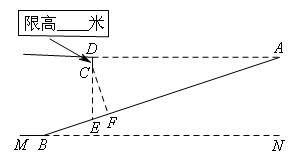
为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度
i=1:3,AD=9米,C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高( )米.
(结果精确到0.1米,参考数据: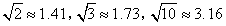 )
)
- A.
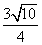
- B.2.37
- C.2.3
- D.2.4
答案
正确答案:C
知识点:解直角三角形的应用
1.解题要点
①要判断限高多少米,需要先求出CF的长,调用测量类应用题做题套路,将CF放到Rt△CEF中求解.
②此题在答题卡上答题时,第一部分是准备条件(将解三角形要用的条件进行说明);第二部分是解直角三角形(在直角三角形中求解);第三部分是总结作答.
③在最后的结果确定上,要注意是用“四舍五入法”,“去尾法”还是“进一法”.
需要根据题意,联系生活实际.
“去尾法”满足最终结果要小于理论计算值,常见于车库限高;
“进一法”满足最终结果要大于理论计算值,比如用油桶装油,理论计算结果4.5个,那就需要用5个.
这道题目需要采用去尾法,否则汽车无法通过.
2.解题过程
如图,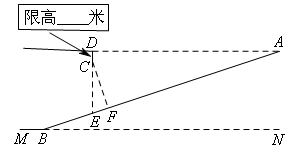
由题意,![]() ,MN∥AD,
,MN∥AD,
∴∠A=∠ABN.
∵AD⊥DE,CF⊥AB,
∴∠A+∠AED=90°,∠AED+∠FCE=90°,
∴∠A=∠FCE,
∴![]() .
.
在Rt△ADE中,![]() ,
,
∴DE=3.
∵CD=0.5,
∴CE=2.5.
在Rt△CEF中,![]() ,
,
∴![]() ,
,
则该停车库限高2.3米.
略








