如图，四边形OABC为直角梯形，OA⊥CO，BC∥OA，OA=CO=4，BC=3．点M从点O出发，以每秒2个单位长度的速度向点A运动；点N从点B同时出发，以每秒1个单位长度的速度向点C运动．当其中一点到达终点时，另一个点也随之停止运动．连接AC，过点N作NP⊥OA于点P，交AC于Q，连接MQ，BQ．

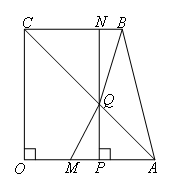
（1）△AQM的面积S与运动时间t之间的函数关系式为(    )

• A.
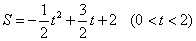
• B.
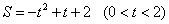
• C.
• D.

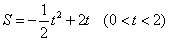
答案

正确答案：B

知识点：动点问题  面积处理思路  

1．解题要点
①研究基本图形，将信息标注在图形上．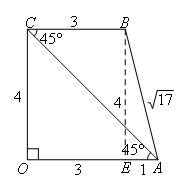

②分析运动状态，分段定范围．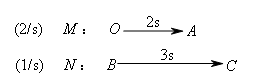

∴．
③分析几何特征、表达、设计方案求解．
由题意得，OM=2t，BN=t，
∴AM=4-2t，CN=NQ=3-t．
∵NP=4，
∴PQ=4-NQ=t+1，
∴．
2．解题过程
如图，

由题意得，NP=CO=OA=4，BC=3，OM=2t，BN=t，
∠BCA=∠OAC=45°，
∴NQ=CN=3-t，AM=4-2t，
∴PQ=4-NQ=t+1，
∴．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>