(上接试题1)(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.易证BD⊥CF.若AB=4, 时,则线段BG的长为( )
时,则线段BG的长为( )

- A.
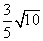
- B.
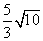
- C.

- D.
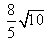
答案
正确答案:D
知识点:等腰直角三角形 正方形的性质 相似三角形的判定和性质 旋转结构
1.解题要点
①结合上一题分析,首先弄清BD⊥CF是怎么证明的.
由△AFC≌△ADB可以得到∠ACF=∠ABD,结合∠CAB=90°可以得到∠BGC=90°,即BD⊥CF;
②分析题目特征,要求线段BG的长,可以先分别求出BD和DG的长.
对于BD,放在△ABD中,结合∠DAB=45°,![]() ,AB=4,通过解这个三角形可以得到BD的长.
,AB=4,通过解这个三角形可以得到BD的长.
对于DG,考虑放在Rt△DGF中,如图,连接DF,易得∠FDN=90°,
∴FD∥AB,
∴∠FDG=∠NBD,△FDG∽△DBN,从而![]() ,可求出
,可求出![]() .
.
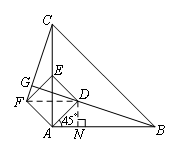
2.解题过程
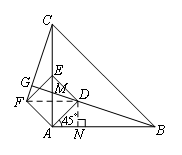
如图,过点D作DN⊥AB于点N,连接DF,设BG与AC交于点M,
由上题可知,∠ABD=∠ACF,
∴∠ACF+∠CMG=∠ABD+∠AMB=90°,
∴BD⊥CF.
由题意,∠BAD=45°,AB=4,![]() ,
,
在Rt△AND中,![]() ,∠ADN=45°,
,∠ADN=45°,
∴BN=AB-AN=3.
在Rt△DNB中,![]() ,
,
在正方形ADEF中,![]() ,
,
∴DF=2,∠FDA=45°,
∴∠FDN=90°,
∴FD∥AB,
∴∠FDG=∠NBD,
∴△FDG∽△DBN,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.
故选D.
略








