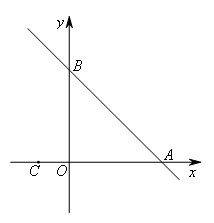
如图,直线y=-x+3与x轴、y轴分别交于A,B两点,点C的坐标为(-1,0),若D为直线AB上一动点,E为坐标平面内一点,且以A,C,D,E为顶点的四边形是正方形,则点D的坐标为( )
- A.

- B.
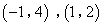
- C.

- D.
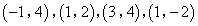
答案
正确答案:B
知识点:正方形的存在性(转等腰直角)
该正方形的存在性可转化为等腰Rt△ACD的存在性,然后通过作两条平行线(或沿等腰直角三角形斜边翻折)找到点E.
∵直线y=-x+3与x轴、y轴分别交于A,B两点,
∴A(3,0),B(0,3),
∴∠OAB=45°.
①当∠ACD=90°时,CA=CD,如图,过点C作CD1⊥x轴,交直线AB于点D1,
则D1(-1,4);
②当∠CDA=90°时,DA=DC,如图,过点C作CD2⊥AB于点D2,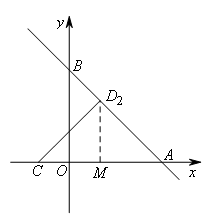
过点D2作D2M⊥x轴于点M,则D2M=AM=CM=2,
∴D2(1,2).
综上,答案选B.
略








