（2009湖南湘西）在直角坐标系xOy中，抛物线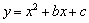与x轴交于两点A、B，与y轴交于点C，其中A在B的左侧，B的坐标是（3，0）．将直线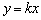沿y轴向上平移3个单位长度后恰好经过点B、C．（1）求k的值；（2）求直线BC和抛物线的解析式；（3）求△ABC的面积；（4）设抛物线顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求点P的坐标．

答案

解：

（1）直线y=kx沿y轴向上平移3个单位后，过两点B，C；
设直线BC的方程为y=kx+3
令x=0，得C（0，3）
又B（3，0）在直线上，
∴0=3k+3∴k=-1
（2）由（1），直线BC的方程为y=-x+3
又抛物线y=x2+bx+c过点B，C
∴解得
∴抛物线方程为
（3）由（2），令得x₁=1，x₂=3
即A（1，0），B（3，0），而C（0，3）
∴△ABC的面积S_ABCABC=（3-1）=3平方单位
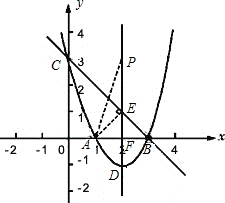
（4）由（2），D（2，-1），
设对称轴与x轴交于点F，与BC交于E，
可得E（2，1），
连接AE．
∵AF=FB=FE=1
∴AE⊥CE，且AE=，CE=（或先作垂线AE⊥BC，再计算也可）
在Rt△AFP与Rt△AEC中，∵∠ACE=∠APE（已知），
∴即，
∴PF=2．
∴点P的坐标为（2，2）或（2，-2）．

知识点：中考压轴之定值问题  

（1）将直线y=kx沿y轴向上平移3个单位后，直线的解析式为y=kx+3，由于这条直线过B、C两点，因此C点的坐标为（0，3），将B点坐标代入直线的解析式后即可求出k的值．
（2）直线BC的解析式在（1）中已求得．根据抛物线过B、C两点，那么可将这两点的坐标代入抛物线的解析式中，用待定系数法求出抛物线的解析式．
（3）根据（2）中得出的抛物线的解析式即可求出A点的坐标，那么△ABC底边AB的长就能求出来了．而△ABC的高OC可根据C点的坐标得出，因此根据三角形的面积计算公式可得出△ABC的面积．
（4）根据（2）得出的抛物线的解析式可求出抛物线的对称轴的解析式．如果设抛物线交BC于E，交x轴于F点．根据对称轴的解析式与BC所在直线的解析式不难得出E点的坐标为（2，1），此时AF=FE=FB，如果连接AE，那么三角形AEB就是个等腰直角三角形．于是三角形AEC也是直角三角形，那么∠ACE和∠APF的正切值就应该相等（已知∠ACE=∠APD），那么可得出的等量关系为AE：CE=AF：PF，据此可求出PF的长，也就能得出P点的坐标．

略

下载次数：6

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>