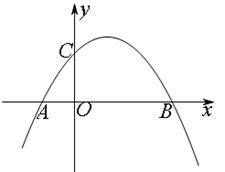
(2009辽宁抚顺)已知:如图所示,关于x的抛物线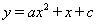 (a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.(1)求出此抛物线的解析式,并写出顶点坐标;(2)在抛物线上有一点D,使四边形ABDC为等腰梯形,写出点D的坐标,并求出直线AD的解析式;(3)在(2)中的直线AD交抛物线的对称轴于点M,抛物线上有一动点P,x轴上有一动点Q.是否存在以A、M、P、Q为顶点的平行四边形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.(1)求出此抛物线的解析式,并写出顶点坐标;(2)在抛物线上有一点D,使四边形ABDC为等腰梯形,写出点D的坐标,并求出直线AD的解析式;(3)在(2)中的直线AD交抛物线的对称轴于点M,抛物线上有一动点P,x轴上有一动点Q.是否存在以A、M、P、Q为顶点的平行四边形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
答案
解:(1)根据题意,得![]() ,解得
,解得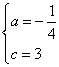
![]() 抛物线的解析式为
抛物线的解析式为![]() 顶点坐标是(2,4)
顶点坐标是(2,4)
(2)![]() 设直线
设直线![]() 的解析式为
的解析式为![]()
![]() 直线经过点
直线经过点![]() 点
点![]()
![]() ,
,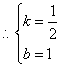 ,
,![]()
(3)存在.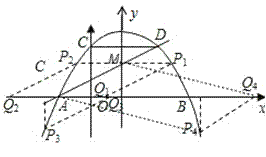
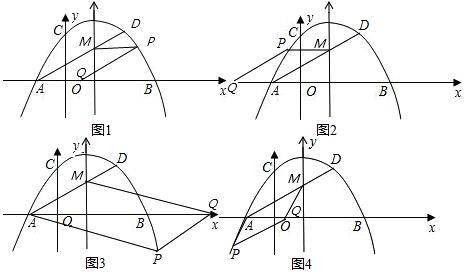
①如图1,P与M的纵坐标相等,可将M的纵坐标代入抛物线中求出P的坐标,然后可根据M,P的横坐标求出MP的长,即AQ的长,然后根据A的坐标即可求出Q的坐标:Q1(2![]() -2,0);
-2,0);
②如图2,方法同①,Q2(-2![]() -2,0);
-2,0);
③如图4,根据平行四边形的对称性,那么M,P的纵坐标互为相反数,因此可求出P的坐标,可先在三角形AOM中求出AO的长,然后A到抛物线对称轴的长+P的横坐标=Q的横坐标,据此可求出Q点的坐标:Q3(6-2![]() ,0);
,0);
④如图3,可参照③的方法求出P的坐标,然后求出PA的长,即MQ的长,然后可过D作x轴的垂线,通过构建直角三角形求出OQ的长.进而得出Q的坐标:Q4(6+2![]() ,0).
,0).
知识点:中考压轴之四边形存在性问题
(1)可将A,B两点的坐标代入函数的解析式中,可求出抛物线的解析式.进而求出对称轴的解析式和定点的坐标;(2)由于二次函数和等腰梯形都是轴对称图形,可根据抛物线的对称轴和C点的坐标求出D的坐标.然后用待定系数法求出A,D所在直线的解析式.(3)分四种情况进行讨论.
略








