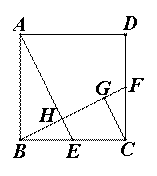
如图，在正方形ABCD中，E、F分别是边BC、CD的中点，AE交BF于点H，CG∥AE交BF于点G．下列结论：①tan∠HBE=cot∠HEB；②CG·BF=BC·CF；③BH=FG；④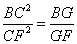．其中正确的序号是（）

①∵在正方形ABCD中，E、F分别是边BC、CD的中点，
∴Rt△ABE≌Rt△BCF，
∴∠BEA=∠CFB，
∵CG∥AE，
∴∠GCB=∠AEB
∴∠CFG=∠GCB，
∴∠CFG+∠GCF=90°即△CGF为直角三角形，
∴CG∥AE交BF于点G，∴△BHE也为直角三角形，
∴tan∠HBE=cot∠HEB；
∴①正确．②由①可得△CGF∽△BCF，
∴，
∴CG•BF=BC•CF，
∴②正确；
③由①得△BHE≌△CGF，
∴BH=CG，而不是BH=FG∴③BH=FG错误；
④∵△BCG∽△BCF，
∴，即BC²=BG•BF，同理CF²=BF•GF，
∴，
∴④正确，综上所述，正确的有①②④．
故选D．

略