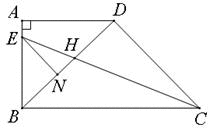
如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD⊥DC，BD=DC，CE平分∠BCD，交AB于点E，交BD于点H，EN∥DC交BD于点N．下列结论：
①BH=DH；
②；
③．
其中正确的是（    ）

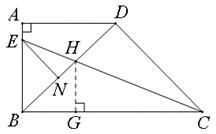
过H做HG⊥BC于点G，CE平分∠BCD，BD⊥CD，
△CGH≌△CDH，∴DH=GH, CG=CD
∵在△BGH中，
∴BH>GH，
∴BH>DH
∴①不对
∵△GCH∽△BCE
∴CH/EH=CG/BG
CG=CD
∠CBD=45°，∴△BGH为等腰直角三角形，BG=GH=DH，BG/BH=1:；
BG：CG=BG：BD=BG：(BH+DH)=BG：(BH+BG)=1：(1+)=EH：CH,
∴②正确，CH=(1+)EH
③△ENH和△EBH同高，高都等于E到BH的距离，底不同。S△ENH：S△EBH=NH：BH
BG：CG=1：(1+)，CG：BC=1：，GH：BE=1：，∴BH=BE=DN，
BH=NH+BN=NH+HD
NH：BH=NH：DN，
NH：DH=EH：CH
∴NH：DN=EH：CE
③正确

略