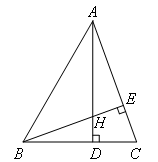
已知：如图，在△ABC中，∠BAC=50°，∠ABC=60°，AD⊥BC，BE⊥AC，垂足分别为D，E，AD，BE相交于点H，则∠AHB的度数是(    )

要求∠AHB的度数，可以把这个角看作是△BDH的外角，
由AD⊥BC，得∠ADB=90°，需求出∠HBD的度数．
又由BE⊥AC，得∠BEC=90°，只需求出∠C的度数即可．
可以把∠C放在△ABC中，由三角形内角和等于180°，
∠BAC=50°，∠ABC=60°，所以∠C=180°-∠BAC-∠ABC=70°．
所以∠HBD=90°-70°=20°，∠AHB=90°+20°=110°．
故选B．

略