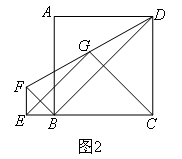
（上接第4题）（2）在图1的基础上，将△BEF绕点B旋转，使点E在CB的延长线上，其他条件不变，如图2，则EG和CG之间的数量和位置关系为( )
- A.EG=CG，但EG与CG不垂直
- B.EG
CG，EG⊥CG - C.EG=CG，EG⊥CG
- D.EG
CG，但EG与CG不垂直
答案
正确答案：C
知识点：类比探究 全等三角形的判定和性质
要类比第（1）问的辅助线和思路，我们先来看第一问的辅助线和思路
带给我们什么．由平行夹中点结构考虑延长之后证全等．
其次证明△CBE≌△CDH（SAS），可以得到△ECH是等腰直角三角形，
得到EG=CG且EG⊥CG．
类比第（1）问的路线图进行证明，先找平行夹中点结构，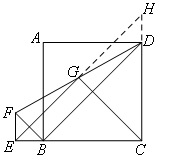
证明△EFG≌△HDG，在此题中△CBE和△CDH是不存在的，
但是可以直接利用EC=HC判断△ECH是等腰直角三角形．
这道题的路线图为：延长EG，交CD的延长线于点H
→△EFG≌△HDG→EF=HD，EG=HG→EC=HC→EG=CG且EG⊥CG．
故选C．
略
WORD格式（
