如图,AB∥CD,∠BAE=40°,∠DCE=50°,求∠E的度数.
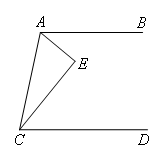
解:如图,
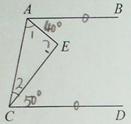
∵AB∥CD(已知)
∴∠BAC+ =180°( )
即∠BAE+∠1+∠2+∠DCE=180°
∵∠BAE=40°,∠DCE=50°(已知)
∴∠1+∠2=180°-∠BAE-∠DCE
=180°-40°-50°
=90°(等式的性质)
在△ACE中,
∴∠E=180°-(∠1+∠2)
=180°-90°
=90°( )
①∠C;②∠ACD;③两直线平行,同旁内角互补;④同旁内角互补,两直线平行;
⑤∠1+∠2=90°;⑥∠1=50°,∠2=40°;⑦平角的定义;⑧三角形的内角和等于180°.
以上空缺处依次所填正确的是( )
- A.②③⑤⑧
- B.①③⑥⑧
- C.①④⑤⑦
- D.②③⑥⑧
答案
正确答案:A
利用AB∥CD,求出∠BAC+∠ACD=180°;结合∠BAE与∠DCE的度数,可以求出∠1+∠2;最后在在△ACE中,利用三角形的内角和等于180°可求出∠E的度数.
第一个空:条件是AB∥CD,结论是∠BAC+______=180°,由平行得到两个角的和等于180°,因此考虑∠BAC的同旁内角,为∠ACD,②正确;
第二个空:条件是AB∥CD,结论是同旁内角互补,因此依据是两直线平行,同旁内角互补,③正确.
第三个空:条件是在△ACE中,____,结合结论∠E=180°-(∠1+∠2)中用到的条件,所以应为∠1+∠2=90°,⑤正确;
第四个空:条件是△ACE中,已知两角的和,结论是求出另外一个角的度数,所以依据是三角形的内角和等于180°,⑧正确.
综上所述,②③⑤⑧正确,故选A.
略









