已知：如图，在△ABC中，AD平分∠BAC，E为AD上一点，且EF⊥BC于F．若∠B=30°，
∠C=70°，求∠DEF的度数．

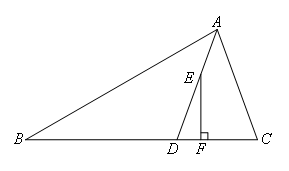
解：如图，
∵在△BAC中，∠B=30°，∠C=70°（已知）
∴∠BAC=180°-∠B-∠C
       =180°-30°-70°
       =80°（三角形的内角和等于180°）
∵AD平分∠BAC（已知）
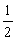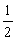∴∠BAD=∠BAC=×80°=40°（角平分线的定义）

∵EF⊥BC（已知）
∴∠EFD=90°（垂直的定义）
∴∠DEF=90°-∠ADF
       =90°-70°
       =20°（直角三角形两锐角互余）
横线处应填写的过程最恰当的是(    )

A.
∴∠BDA=180°-∠B-∠BAD
=180°-30°-40°
=110°（三角形的内角和等于180°）
B.
∵∠ADF=∠BAD+∠B（外角的定义）
∴∠ADF=40°+30°
=70°（三角形的一个外角等于和它不相邻的两个内角的和）
C.
∴∠DAC=40°（等量代换）
D.
∵∠ADF是△ABD的一个外角（外角的定义）
∴∠ADF=∠BAD+∠B
=40°+30°
=70°（三角形的一个外角等于和它不相邻的两个内角的和）

答案

正确答案：D

第一步：读题标注，如图，

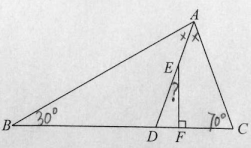
第二步：走通思路，要求∠DEF的度数，怎么想？
要求∠DEF的度数，可以将∠DEF放在Rt△DEF中，
利用直角三角形两锐角互余，得到∠DEF+∠EDF=90°，
因此只需求出∠EDF，即∠ADF的度数即可；
∠ADF可以看成△ABD的一个外角，
利用三角形的一个外角等于和它不相邻的两个内角的和，
得∠ADF=∠BAD+∠B，
已知∠B=30°，因此下一步的目标是求∠BAD的度数；
结合已知条件∠B=30°，∠C=70°，
在△ABC中利用三角形的内角和等于180°，求出∠BAC=80°，
又AD平分∠BAC，利用角平分线的定义，得∠BAD=40°；
那么∠ADF=∠BAD+∠B=70°，∠DEF=90°-∠ADF=20°．
第三步：规划过程；
根据分析，过程主要分为四个书写模块：
①在△BAC中，利用三角形内角和定理求出∠BAC的度数；
②利用角平分线的定义求出∠BAD的度数；
③利用三角形外角定理，求出∠ADF的度数；
④最后利用直角三角形两锐角互余，求出∠DEF的度数．
故选D．

略

下载次数：0

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>