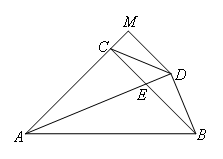
如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC
交AC的延长线于M，连接CD，给出三个结论：①∠ADC=45°；②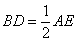；③AC+CE=AB；其中正确的结论有(    )

如图，延长BD交AC的延长线于点F，过点E作EG⊥AB于点G，

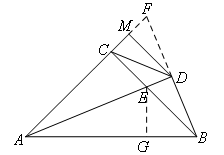
∵AE平分∠BAC，AE⊥BD，
∴△BAF是等腰三角形，
∴，
∵AD⊥BD
∴∠BDA=∠ACB=90°，
∵∠CEA=∠DEB，∠CEA+∠CAE=∠DEB+∠DBE=90°
∴∠CAE=∠DBE，
又∵AC=CB
∴△ACE≌△BCF（ASA），
∴AE=BF
∴，故②正确；
由题意可知，∠CBD=∠CAD=22.5°
∵点D是Rt△BCF斜边中点，
∴CD=DB=DF
∴∠DCB=∠DBC=22.5°
∴∠CDF=45°
∴∠ADC=45°，故①正确；
∵AE平分∠BAC
∴CE=EG，
∵∠EBG=45°
∴GB=EG=CE
易证△ACE≌△AGE（AAS），
∴AC=AG
∴AB=AG+GB=AC+CE，故③正确；
综上，三个结论都是正确的．
故选D．

略