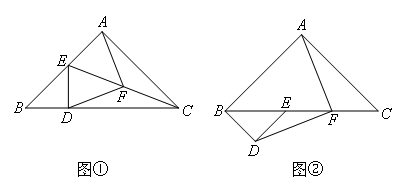
已知等腰直角三角形ABC中,D为斜边BC上一点,过D点作DE⊥BC交AB于E,连接CE,
F为CE中点,连接AF,DF,易证AF=DF;
(1)若将图①中△BDE绕点B顺时针旋转45°,如图②所示,取CE的中点F,连接AF,DF,则下列结论中错误的是( )
- A.
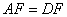
- B.
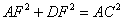
- C.
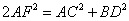
- D.
答案
正确答案:B
知识点:类比探究问题
1.思路分析
①分析题干中的易证,点F是CE的中点,AF和DF分别是Rt△ACE和Rt△DCE斜边的中线,则![]() .
.
②第一问,分析可得,△ABC和△BDE均为等腰直角三角形,点F是CE的中点,考虑类倍长中线,如图,延长AF到M,使FM=AF,连接EM,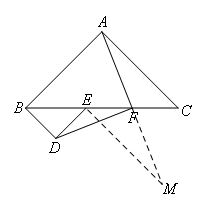
易证△ACF≌△MEF,得到AF=FM,AC=EM,∠FEM=∠C=45°,
可得∠DEM=90°,考虑连接AD,DM,易证△ABD≌△MED,
可得,AD=DM,易得∠ADM=90°,则△ADM是等腰直角三角形,
得到AF=DF且AF⊥DF,分别在Rt△ABD和Rt△ADF中利用勾股定理可得,![]() .
.
梳理线路图如图所示: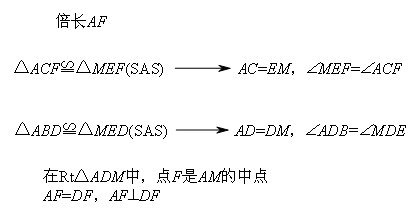
2.解题过程
如图,延长AF到M,使FM=AF,连接EM,AD,DM.
分析可知,△ABC和△BDE均为等腰直角三角形.
易证△ACF≌△MEF(SAS),可得,AF=FM,AC=EM,∠FEM=∠C=45°,
∴AB=AC=EM,∠DEM=180°-∠BED-∠FEM=90°,
又∵BD=DE
∴△ABD≌△MED(SAS)
∴AD=DM,∠ADB=∠MDE,
∵∠ABD+∠ADE=90°,
∴∠MDE+∠ADE=90°,
∴△ADM是等腰直角三角形,
∵点F是斜边AM的中点,
∴AF=DF=FM,且AF⊥DF,故选项A,D正确;
在Rt△ABD和Rt△ADF中,
由勾股定理可得,![]() ,
,![]()
∴![]() ,故选项C正确;
,故选项C正确;
∵线段BD的长度不为0,
∴![]() 不成立.选项B错误;
不成立.选项B错误;
故选B.
略








