如图,在△ABC中,AB=AC=8,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的平分线,
DF∥AB交AE延长线于F,则DF的长为( )
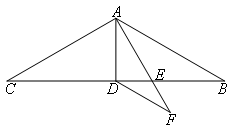
- A.2
- B.4
- C.5
- D.6
答案
正确答案:B
分析:
由AB=AC,AD是△ABC的中线,可得AD⊥BC;
由AE平分∠BAD,DF∥AB,可得∠DAF=∠F,所以AD=DF;
要求DF的长就转化成求AD的长.
由AB=AC,∠BAC=120°,可得∠B=30°;
由∠B=30°,AD⊥BC,AB=8,可得![]() .
.
解题过程:
∵AB=AC,AD是△ABC的中线
∴AD⊥BC
∵AE是∠BAD的平分线
∴∠DAE=∠BAE
∵DF∥AB
∴∠F=∠BAE
∴∠DAE=∠F
∴AD=DF
∵∠BAC=120°,AB=AC
∴∠B=30°
∵AD⊥BC,AB=8
∴![]()
故选B
略








