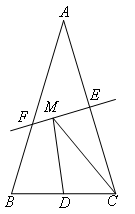
如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF交AB边于点F，交AC边于点E．若点D为BC边的中点，M为线段EF上一动点，则△CDM周长的最小值为(    )

分析特征：有动点（M），有定点（C，D），并且动点（M）在定直线（EF）
上运动，求线段和最小，符合轴对称—最值问题的特征．
因此作定点关于定直线的对称点，如图，点C与点A关于直线EF对称，
连接AD交EF于点M，则点M即为所求，连接CM，
此时△CDM的周长最小．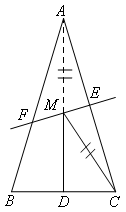

因为EF垂直平分AC，点D为等腰三角形ABC底边的中点，
所以AD⊥BC，AM=CM，
所以△CDM的周长为CD+DM+CM=CD+DM+AM=CD+AD，
因此只需要求出AD的长即可．
根据底边BC长为4，面积是16，可求AD=8，
因此△CDM周长的最小值为2+8=10．
故选C

略