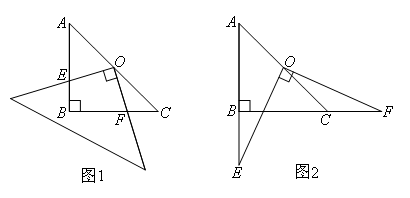
如图,在Rt△ABC中,AB=BC,∠ABC=90°.一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,图1,图2是旋转三角板所得图形的两种情况,三角板的两直角边分别交AB,BC或其延长线于点E,F,图1,图2可以证明出OE与OF之间有相同的数量关系,则这个数量关系为( )
- A.
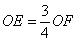
- B.
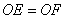
- C.
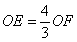
- D.
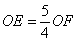
答案
正确答案:B
知识点:类比探究问题
观察到两问都有中点,且是直角加中点,所以考虑利用直角三角形斜边的中线等于斜边一半进行类比,如图,
OE=OF,证明如下:
如图1,连接BO,
∵BO是等腰Rt△ABC斜边的中线,
∴BO=OA=OC,BO⊥AC,∠OBA=∠OCB=45°,
又∵∠EOF=90°,
∴∠BOE=∠COF,
∴△BOE≌△COF(ASA),
∴OE=OF.
如图2,连接BO,
∵BO是等腰Rt△ABC斜边的中线,
∴BO=OA=OC,BO⊥AC,∠OBA=∠OCB=45°,
又∵∠EOF=90°,
∴∠BOE=∠COF,
∵∠OBA=∠OCB=45°,
∴∠OBE=∠OCF=135°,
∴△BOE≌△COF(ASA),
∴OE=OF.
故选B.
略








