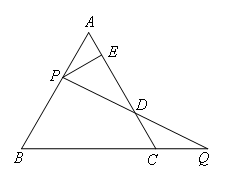
如图,过边长为6的等边三角形ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC于D,则DE的长为( )
- A.1
- B.
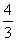
- C.2
- D.3
答案
正确答案:D
如图,
过P作PF∥BC交AC于F,
∵PF∥BC,△ABC是等边三角形,
∴△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ,
∵PF∥BC,
∴∠PFD=∠QCD,∠FPD=∠CQD,
∴△PFD≌△QCD(ASA)
∴FD=CD,
∴AC=AE+EF+FD+CD=2(EF+FD)=2DE,
∵AC=6,
∴DE=3
故选D
略








