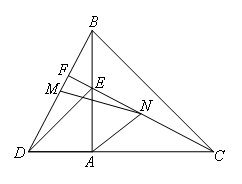
如图，△ABC与△ADE都是等腰直角三角形，∠BAC=∠DAE=90，按A，D，C在同一条直线上，直线CE交BD于点F，连接AF，点M，N分别是BD，CE的中点，有下列说法：①BD=CE；②CF⊥BD；③AF平分∠DFC；④△AMN是等腰直角三角形．其中正确的结论是(    )

如图，
∵△ABC与△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，
∴AB=AC，AD=AE
∴△DAB≌△EAC（SAS）
∴BD=CE，∠DBA=∠ACE，故①正确；
∵∠BAC=90°
∴∠ACE+∠AEC=90°，
∵∠AEC=∠BEF
∴∠BEF+∠DBA=90°，
∴∠BFE=90°，即CF⊥BD，故②正确；
如图，连接AF，过点A作AG⊥BD于点G，AH⊥CE于点H，

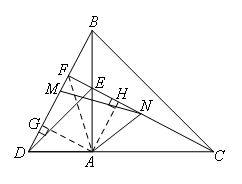
易证△ADG≌△AEH（AAS）
∴AG=AH，
∴点A在∠DFC的角平分线上，即AF平分∠DFC，故③正确；
如图，连接AM，

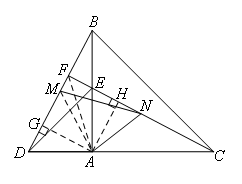
在等腰直角三角形△ABC与△ADE中，∠BAC=∠DAE=90°，
点M，N分别是BD，CE的中点，
∴
∴AM=AN，∠MAB=∠ABD，∠NAE=∠AEC，
∵∠ABD=∠ACE，∠ACE+∠NAE=90°，
∴∠MAB+∠NAE=90°，即∠MAN=90°，
∴△AMN是等腰直角三角形，④正确；
综上，四个结论都正确，故选D

略