如图,已知A,B是反比例函数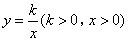 图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)向终点C匀速运动.过点P作PM⊥x轴于点M,PN⊥y轴于点N,设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)向终点C匀速运动.过点P作PM⊥x轴于点M,PN⊥y轴于点N,设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )

- A.
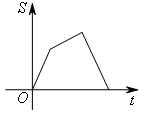
- B.
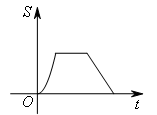
- C.

- D.

答案
正确答案:B
由题意得,四边形OMPN为矩形,![]() .
.
根据点P运动状态的转折可确定函数图象需分三段研究:
法一:首先分析容易分析的第二段,此时点P在反比例函数图象上运动,结合反比例函数的面积不变性,此时S大小不变,排除选项A、选项D;
再分析第三段,此时四边形为矩形,且矩形的长不变,宽随点P的运动而逐渐变小,排除选项C,答案选B.
法二:
①当点P在线段OA上时,设点P的运动速度为![]() (
(![]() 为常数),∠AOM=
为常数),∠AOM=![]() (α为定值).
(α为定值).
在Rt△OMP中,![]() ,
,![]() ,
,
∴![]() ,函数图象为抛物线的一部分,开口向上.
,函数图象为抛物线的一部分,开口向上.
②当点P在双曲线上运动时,由反比例函数的面积不变性可得,![]() .
.
③当点P在BC上运动时,PM=OC,长度不变,OM随着点P的运动变小,
所以S随t的增大而减小.
故选B.
略








