学生做题前请先回答以下问题

问题1:绝对值的定义：在       上，一个数所对应的    与      的       叫做这个数的绝对值．

问题2:一个数的绝对值与这个数有什么关系？

问题3:（上接第2题）根据一个数的绝对值与和这个数的关系，所以在去绝对值时，首先要判断绝对值内整体的符号．比如：要化简，首先要判断的正负，然后再去绝对值．
例：已知，化简．

问题4:去绝对值的操作步骤一般是：①看整体，        ；②依法则，        ；③去括号，合并．

问题5:若，则之间满足什么关系？

问题6:已知，，且，求的值．
绝对值分类讨论的操作步骤：①画树状图，分类；②根据限制条件，筛选、排除．请按照这个步骤进行操作．

代数推理综合练习（绝对值）（人教版）

单选题(本大题共小题， 共分)

1.(本小题10分) 已知，则下列说法正确的是(    )
    2.(本小题10分) 有理数在数轴上的对应点如图所示，则化简的结果为(    )
      3.(本小题10分) 有理数在数轴上的对应点如图所示，化简的结果为(    )
        4.(本小题10分) 已知，化简的结果为(    )
          5.(本小题10分) 已知，，，化简的结果为(    )
            6.(本小题10分) 关于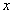的方程的解是(    )
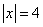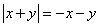              7.(本小题10分) 已知，，且，则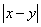的值为(    )
                8.(本小题10分) 若，则的取值共有(    )
                  9.(本小题10分) 结合数轴与绝对值的知识回答下列问题：
                  数轴上4和1两点之间的距离是     ；-3和2两点之间的距离是     ；一般地，数轴上数和数n两点之间的距离等于，如果数和-2两点之间的距离是3（在数轴上，数在原点的左边），那么     ．
                  以上空缺处依次所填正确的是(    )
                    10.(本小题10分) 若为有理数，则的最小值为(    )

                      学生做题后建议通过以下问题总结反思

                      问题1：绝对值的定义：在       上，一个数所对应的    与      的       叫做这个数的绝对值．

                      问题2：一个数的绝对值与这个数有什么关系？

                      问题3：（上接第2题）根据一个数的绝对值与和这个数的关系，所以在去绝对值时，首先要判断绝对值内整体的符号．比如：要化简，首先要判断的正负，然后再去绝对值．
                      例：已知，化简．

                      问题4：去绝对值的操作步骤一般是：①看整体，        ；②依法则，        ；③去括号，合并．

                      问题5：若，则之间满足什么关系？

                      问题6：已知，，且，求的值．
                      绝对值分类讨论的操作步骤：①画树状图，分类；②根据限制条件，筛选、排除．请按照这个步骤进行操作．