1.(本小题20分) 如图1所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点，连接AM，AN，MN．
（1）求证：①BE=CD；②△AMN是等腰三角形．

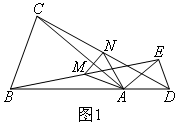
下面给出了证明的路线图：
`
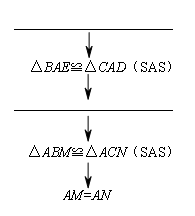①AB=AC，∠AEB=∠ADC，AE=AD；②AB=AC，∠BAE=∠CAD，AE=AD；③BA=CA，∠ABM=∠ACN，BM=CN；
④BA=CA，∠ABM=∠ACN，∠AEB=∠ADC；⑤BA=CA，∠ABM=∠ACN，EM=DN．
以上横线处，依次所填正确的是(    )

核心考点: 类比探究  全等三角形的判定和性质 

3.(本小题20分) （1）如图1，在正方形ABCD的边AB上任取一点E，过点E作EF⊥AB，交BD于点F，取DF的中点G，连接EG，CG．求证：EG=CG，EG⊥CG．

如图1-1，

下面给出了证明的路线图：

①△EFG≌△HDG；②△CBE≌△CDH；③EF=DH；④EF=DH，EG=HG；⑤EG=HG；
⑥EC=HC，∠1=∠2；⑦∠1=∠2．
以上横线处，依次所填正确的是(    )

核心考点: 类比探究  全等三角形的判定和性质 

5.(本小题20分) （上接第3，4题）（3）在图1的基础上，将△BEF绕点B旋转，使点E在AB的延长线上，其他条件不变，如图3，为了证明EG和CG之间的数量和位置关系，类比（1），（2）中的辅助线和证明思路，需要作出的辅助线是(    )

核心考点: 类比探究  全等三角形的判定和性质