实际生活应用问题(三)(结果判断)
满分100分 答题时间40分钟
已经有598位用户完成了练习
单选题(本大题共小题, 共分)
-
6.(本小题15分)
身高1.65米的小刚在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,小刚位于建筑物前的点B处,风筝挂在建筑物上方树枝上的点G处(点G在FE的延长线上).经测量,小刚与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.则风筝距地面的高度GF为 米;若在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,则小刚充分利用梯子和一根5米长的竹騀, (填“能”或“不能”)触到挂在树上的风筝.( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
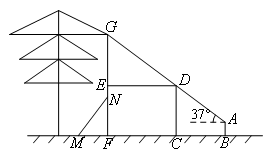
核心考点: 解直角三角形的应用 三角函数、实际应用题








