角的相关计算和证明过程训练(平行、外角)(二)(北师版)
满分100分 答题时间30分钟
已经有533位用户完成了练习
单选题(本大题共小题, 共分)
-
1.(本小题14分)
请根据过程示范,完成下题.
例题:
已知:如图,AB∥CD,BE交CD于点F,∠D=24°,∠E=21°,求∠B的度数.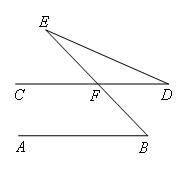
过程示范如下:
解:如图,
∵∠EFC是△EFD的一个外角(外角的定义)
∴∠EFC=∠E+∠D(三角形的一个外角等于和它不相邻的两个内角的和)
∵∠D=24°,∠E=21°(已知)
∴∠EFC=21°+24°=45°(等量代换)
∵AB∥CD(已知)
∴∠B=∠EFC(两直线平行,同位角相等)
∴∠B=45°(等量代换)
问题:
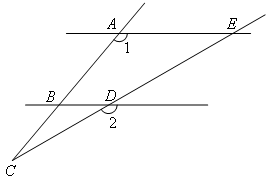
已知:如图,AB∥CD,点G在AB上,EG与CD交于点F,∠E=40°,∠D=26°,求∠AGE的度数.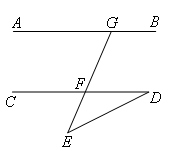
解:如图,
∵ (外角的定义)
∴ ( )
∵∠E=40°,∠D=26°(已知)
∴∠GFD=40°+26°=66°(等量代换)
∵AB∥CD(已知)
∴ ( )
∴∠AGE=66°(等量代换)
①∠GFD是△FED的一个外角;②∠GFD=∠E+∠D;③∠CFE=∠E+∠D;④外角的定义;
⑤三角形的一个外角等于和它不相邻的两个内角的和;⑥∠AGE=∠GFD;⑦∠AGE=∠CFE;
⑧两直线平行,内错角相等;⑨两直线平行,同位角相等.
以上空缺处依次所填正确的是( )
核心考点: 平行线的性质 三角形的外角
-
6.(本小题15分)
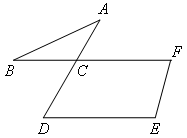
已知:如图,AD与EB,FC分别相交于点G,H,∠E+∠F=180°.
求证:∠A+∠B+∠C+∠D=180°.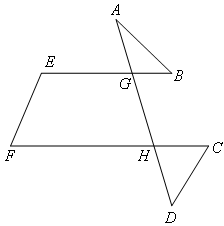
证明:如图,
∵∠E+∠F=180°(已知)
∵∠GHC是△HDC的一个外角(外角的定义)
∴∠GHC=∠C+∠D(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠A+∠B+∠C+∠D=180°(等量代换)
①∵∠BGH是△AGB的一个外角(外角的定义)
②∵∠BGH=∠A+∠B(外角的定义)
③∴∠BGH=∠A+∠B(三角形的一个外角等于和它不相邻的两个内角的和)
④∴EB∥FC(同旁内角互补,两直线平行)
⑤∴EB∥FC(两直线平行,同旁内角互补)
⑥∴∠BGH+∠GHC=180°(两直线平行,同旁内角互补)
⑦∴∠BGH+∠GHC=180°(同旁内角互补,两直线平行)
横线处应填写的过程,顺序正确的是( )
核心考点: 平行线的判定 平行线的性质 三角形的外角
-
7.(本小题15分)
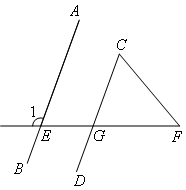
已知:如图,EN交AB于M,EH交AB于G,∠1=∠2,∠3=30°,∠EHC=55°,求∠EFG的度数.
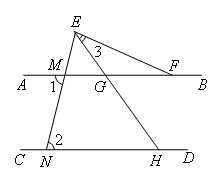
解:如图,
∵∠1=∠2(已知)
∴∠EFG=∠EGA-∠3
=55°-30°
=25°(等式性质)
①∵∠3=30°(已知)
②∵∠EHC=55°(已知)
③∵∠EGA是△EGF的一个外角(外角的定义)
④∵∠EGA=∠3+∠EFG(外角的定义)
⑤∴AB∥CD(内错角相等,两直线平行)
⑥∴AB∥CD(两直线平行,内错角相等)
⑦∴∠EGA=∠EHC(两直线平行,同位角相等)
⑧∴∠EGA=55°(等量代换)
⑨∴∠EGA=∠3+∠EFG(三角形的一个外角等于和它不相邻的两个内角的和)
横线处应填写的过程,顺序正确的是( )
核心考点: 平行线的判定 平行线的性质 三角形的外角