角的相关计算和证明过程训练(综合)(三)(北师版)
满分100分 答题时间30分钟
已经有513位用户完成了练习
单选题(本大题共小题, 共分)
-
3.(本小题20分)
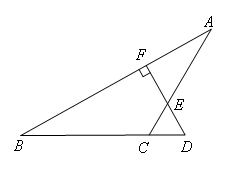
已知:如图,在△ABC中,AD平分∠BAC,E为AD上一点,且EF⊥BC于点F.
若∠C=35°,∠1=15°,求∠B的度数.
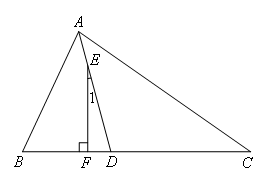
解:如图,
∵∠EDF是△ADC的一个外角(外角的定义)
∴∠EDF=∠DAC+∠C(三角形的一个外角等于和它不相邻的两个内角的和)
∵∠C=35°(已知)
∴∠DAC=∠EDF-∠C
=75°-35°
=40°(等式性质)
∵AD平分∠BAC(已知)
∴∠BAC=2∠DAC=2×40°=80°(角平分线的定义)
∴∠B=180°-∠BAC-∠C
=180°-80°-35°
=65°(三角形的内角和是180°)
横线处应填写的过程最恰当的是( )
核心考点: 三角形内角和定理 直角三角形两锐角互余 三角形的外角
-
4.(本小题20分)
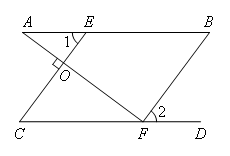
已知:如图,在△ABC中,EF∥AD,∠EFD=80°,∠1=20°,∠2=50°,求∠DGC的度数.
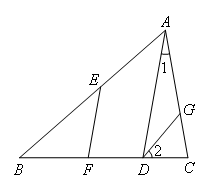
解:如图,
∴∠ADG=∠ADC-∠2
=80°-50°
=30°(等式性质)
∵∠DGC是△ADG的一个外角(外角的定义)
∴∠DGC=∠1+∠ADG(三角形的一个外角等于和它不相邻的两个内角的和)
∵∠1=20°(已知)
∴∠DGC=20°+30°
=50°(等量代换)
横线处应填写的过程,顺序正确的是( )
①∵EF∥AD(已知)
②∵∠EFD=80°(已知)
③∵∠2=50°(已知)
④∴∠ADC=80°(等量代换)
⑤∴∠ADC=∠EFD(两直线平行,同位角相等)
⑥∴∠ADF=180°-∠EFD=100°(两直线平行,同旁内角互补)
核心考点: 平行线的性质 三角形外角定理