1.(本小题16分) 为推进节能减排，发展低碳经济，我市某“用电大户”用480万元购得“变频调速技术”后，进一步投入资金1520万元购买配套设备，以提高用电效率，达到节约用电的目的．已知该“用电大户”生产的产品每件成本费为40元．经过市场调研发现：该产品的销售单价，需定在100元到300元之间较为合理．当销售单价定为100元时，年销售量为20万件；当销售单价超过100元，但不超过200元时，每件产品的销售价格每增加10元，年销售量将减少0.8万件；当销售单价超过200元，但不超过300元时，每件产品的销售价格每增加10元，年销售量将减少a万件．设销售单价为x（元），年销售量为y（万件），年获利为w（万元）．
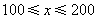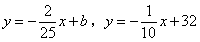（1）若求出当，时，y与x之间的函数关系式分别是，则a，b的值分别为(    )

核心考点: 一次函数的应用  函数类应用题 

核心考点: 二次函数的应用  函数类应用题 

5.(本小题18分) （上接第4题）（2）如图，直线y=kx+1交x轴于点D，交y轴于点E，交抛物线于点F，G．点P是y轴上一点且使得以P，C，F，G为顶点的四边形是平行四边形，则k的值为(    )

核心考点: 二次函数与几何综合  平行四边形的存在性