1.(本小题14分) 已知：如图，AB∥CD，AD∥BC．
求证：∠A=∠C．

证明：如图，
∵AB∥CD（已知）
∴∠B+∠C=180°（两直线平行，同旁内角互补）
∵AD∥BC（已知）
∴∠B+∠A=180°（                            ）
∴∠A=∠C（                            ）
请你仔细观察下列序号所代表的内容：
①等角或等角的余角相等；②同角或等角的补角相等；③等量代换；
④两直线平行，同旁内角互补；⑤同旁内角互补；
⑥同旁内角互补，两直线平行．
以上空缺处依次所填正确的是(    )

核心考点: 平行线的性质 

3.(本小题14分) 已知：如图，BD⊥AC于点D，EF⊥AC于点F，G是AB上一点，
且∠l=∠2．
求证：GD∥BC．

证明：如图，

∵BD⊥AC，EF⊥AC（已知）
∴∠BDC=∠EFC=90°（垂直的定义）
∴BD∥EF（                      ）
∴∠2=∠3（                      ）
∵∠l=∠2（已知）
∴∠1=∠3（                      ）
∴GD∥BC（内错角相等，两直线平行）
请你仔细观察下列序号所代表的内容：
①同位角相等，两直线平行；②两直线平行，同位角相等；
③内错角相等；④两直线平行，内错角相等；⑤等量代换；
⑥等式的性质．
以上空缺处依次所填正确的是(    )

核心考点: 平行线的判定  平行线的性质  垂直的定义 

5.(本小题14分) 如图：AC∥ED，AB∥FD，∠A=54°，求∠EDF的度数．
推理过程如下：

解：如图，
∵AB∥FD（已知）
∴      =∠DFC（两直线平行，同位角相等）
∵AC∥ED（已知）
∴      =∠EDF（两直线平行，内错角相等）
∴∠EDF=∠A（等量代换）
∵∠A=54°（已知）
∴∠EDF=54°（等量代换）
以上空缺处依次所填正确的是(    )

核心考点: 平行线的性质与判定 

7.(本小题15分) 已知：如图，点E，F分别在AB，CD上，AF⊥CE，垂足为点O，∠1=∠B，
∠A+∠2=90°．
求证：AB∥CD．

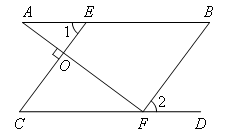
证明：如图，
∵∠1=∠B（已知）
∴CE∥BF（同位角相等，两直线平行）
                             
∴∠AFC+∠2=90°（等式性质）
∵∠A+∠2=90°（已知）
∴∠AFC=∠A（同角或等角的余角相等）
∴AB∥CD（内错角相等，两直线平行）
请你仔细观察下列序号所代表的内容：
①∴∠AOE=90°（垂直的定义）
②∴∠AFB=90°（等量代换）
③∵AF⊥CE（已知）
④∵∠AFC+∠AFB+∠2=180°（平角的定义）
⑤∴∠AOE=∠AFB（两直线平行，同位角相等）
横线处应填写的过程，顺序正确的是(    )

核心考点: 平行线的判定  平行线的性质  同角或等角的余角相等