类比探究（五）
满分100分 答题时间30分钟
已经有586位用户完成了练习
单选题(本大题共小题， 共分)
-
1.(本小题16分)
（1）问题背景：
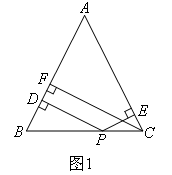
如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠D=90°．E，F分别是边BC，CD上的点，
且∠EAF=60°．
求证：EF=BE+DF．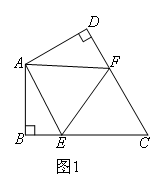
（2）探索延伸：
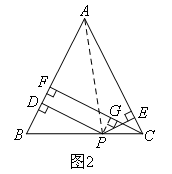
如图2，在四边形ABCD中，AB=AD，E，F分别是边BC，CD上的点，且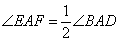
，则当∠B和∠D满足什么条件时，EF=BE+DF成立？
（3）实际应用：
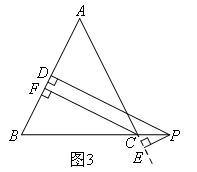
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进．1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，则此时两舰艇之间的距离为( )海里．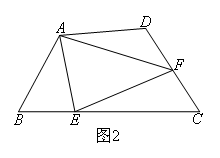
（建议学生先打印纸质材料，再做题）
（1）中证明上述结论的辅助线的作法，有如下说法：①延长FD到G，使DG=BE，连接AG；
②过点A作AG⊥EF于点G；
③将△ABE绕点A逆时针旋转120°得到△ADG（之后证明点G，D，F在同一条直线上）．
其中可以证明结论的是( )
，则当∠B和∠D满足什么条件时，EF=BE+DF成立？
核心考点: 类比探究问题 全等三角形的判定与性质
-
4.(本小题17分)
[问题情境]张老师给爱好学习的小军和小俊提出这样一个问题：如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．
小军的证明思路是：如图2，连接AP，由△ABP与△ACP的面积之和等于△ABC的面积可以证得：
PD+PE=CF．
小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．
[变式探究]如图3，当点P在BC延长线上时，其余条件不变，请探究PD，PE，CF之间的数量关系，并证明该结论．
请运用上述解答中所积累的经验和方法完成下列两题：
[结论运用]如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点
处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BC，垂足分别为G，H．若AD=8，CF=3，求PG+PH的值．
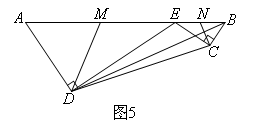
[迁移拓展]图5是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D，C，且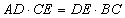
，
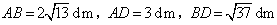．M，N分别为AE，BE的中点，连接DM，CN，求△DEM与△CEN的周长之和．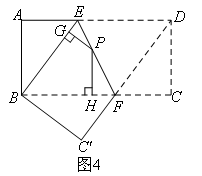
（建议学生先打印纸质材料，再做题）
（1）[变式探究]中PD，PE，CF之间的数量关系为( )
处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BC，垂足分别为G，H．若AD=8，CF=3，求PG+PH的值．
，
．M，N分别为AE，BE的中点，连接DM，CN，求△DEM与△CEN的周长之和．
核心考点: 等腰三角形的性质 全等三角形的判定与性质 等面积法
