中考数学压轴题实战演练（三） -九年级试卷-众享学科测评

中考数学压轴题实战演练（三）

满分22分答题时间30分钟

已经有457位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 已知抛物线经过三点，一动点P从原点出发，以每秒1个单位长度的速度沿x轴正方向运动，连接BP，过点A作直线BP的垂线，交y轴于点Q．设点P运动的时间为t秒． （1）求抛物线的解析式； （2）当BQ=AP时，求t的值； （3）随着点P的运动，在抛物线上存在点M，使△MPQ为等边三角形，请直接写出相应的t值及点M的坐标． （1）中抛物线的解析式为( )

2.(本小题4分) （上接第1题）（2）中当BQ=AP时，t的值为( )

3.(本小题4分) （上接第1，2题）（3）中t的值及点M的坐标分别为( )

4.(本小题3分) 综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A，C两点的坐标分别为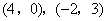，抛物线W经过O，A，C三点，D是抛物线W的顶点． （1）求抛物线W的解析式； （2）将抛物线W和平行四边形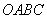一起先向右平移4个单位后，再向下平移m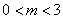（）个单位，得到抛物线W′和平行四边形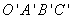，在向下平移的过程中，设平行四边形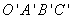与平行四边形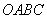重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值； （3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，M是x轴上的动点，N是抛物线W′上的动点，若以D，F，M，N为顶点的四边形是平行四边形，请直接写出点M的坐标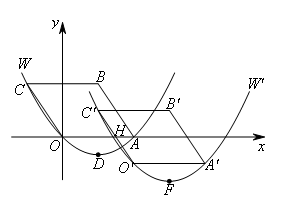． （1）中抛物线W的解析式是( )

5.(本小题4分) （上接第4题）（2）中S的最大值以及S取最大值时m的值分别为( )

6.(本小题4分) （上接第4，5题）（3）中若以D，F，M，N为顶点的四边形是平行四边形，则点M的坐标为( )