1.(本小题20分) 在四边形ABCD中，BA=BC，．
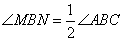（1）如图1，当点M，N分别在AD，CD上时，若∠BAD+∠BCD=180°，求证：MN=AM+CN．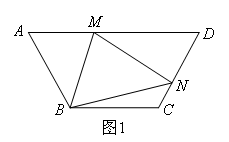

先在图上走通思路后再填写空格内容：
（1）如图，延长NC到E，使CE=AM，连接BE．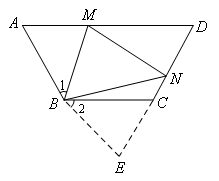

由∠BAD+∠BCD=180°，∠BCE+∠BCD=180°，利用同角的补角相等，得∠BAD=∠BCE；因为BA=BC，AM=CE，因此根据三角形全等的判定           ，可以得到△BAM≌△BCE，由全等的性质得到                      ；
又因为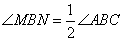，可得             ，因此根据三角形全等的判定SAS，可以得到           ，由全等的性质得MN=EN；所以MN=EN=CE+CN=AM+CN．
请你仔细观察下列序号所代表的内容：
①ASA；②SAS；③SSA；④AM=CE，BM=BE；⑤∠1=∠2，BM=BE；⑥∠1=∠2；⑦∠MBN=∠EBN；⑧△MBN≌△EBN；⑨△BAM≌△MDN．
以上空缺处依次所填最恰当的是(    )

核心考点: 三角形全等之类比探究 

3.(本小题20分) △ABC和△CDE均为等腰直角三角形，∠ABC=∠CDE=90°，AB=BC，DC=DE，CD＞BC，M是AE的中点．
（1）如图1，当点C，B，D在同一直线上，求证：DM⊥BM．

如图，下面给出了证明的路线图：



请你仔细观察下列序号所代表的内容：
①延长BM，交DE于点F，使MF=MB；②延长BM，交DE于点F；③AB=EF，BM=FM；④AM=EM，∠ABM=∠EFM．
以上横线处，依次所填最恰当的是(    )

核心考点: 三角形全等之类比探究 

5.(本小题20分) （上接第4题）（3）题干中的其他条件不变，当BC⊥CE时，要证明MD⊥MB，在4第题添加的辅助线的基础上，要证明△BCD≌△FED，理由是(    )

核心考点: 类比探究  全等三角形的判定和性质