二次函数与几何综合
满分40分 答题时间40分钟
已经有94位用户完成了练习
解答题(本大题共小题, 共分)
-
1.(本小题10分)
如图1,在平面直角坐标系中,二次函数
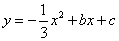 的图象与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒,连接PQ.
的图象与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒,连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图2,点N的坐标为(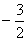 ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.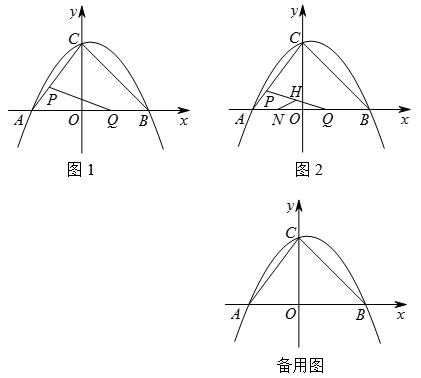
核心考点: 三角形存在性问题 点的存在性问题
-
2.(本小题10分)
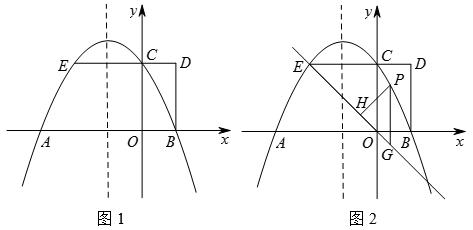
如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边
CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
核心考点: 点的存在性问题 四边形存在性问题





