三角形全等之截长补短(一)(北师版)
满分100分 答题时间30分钟
已经有558位用户完成了练习
单选题(本大题共小题, 共分)
-
2.(本小题25分)
已知,如图,BM平分∠ABC,点P为BM上一点,PD⊥BC于点D,BD=AB+DC.
求证:∠BAP+∠BCP=180°.
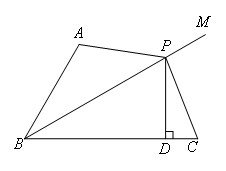
(补短法)证明:如图,
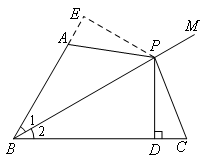
∵BP平分∠ABC
∴∠1=∠2
在△BEP和△BDP中
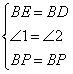
∴△BEP≌△BDP(SAS)
在△PEA和△PDC中
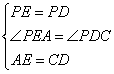
∴△PEA≌△PDC(SAS)
∴∠C=∠PAE
∵∠BAP+∠PAE=180°
∴∠BAP+∠BCP=180°
请你仔细观察下列序号所代表的内容:
①延长BA,过点P作PE⊥BA于点E;②延长BA到E,使AE=DC,连接PE;
③延长BA到E,使DC=AE;④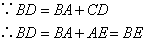 ;⑤
;⑤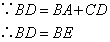 ;
;
⑥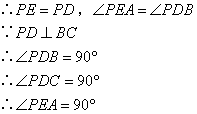 ;⑦
;⑦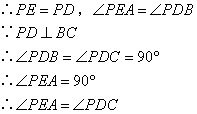 .
.
以上空缺处依次所填最恰当的是( )
核心考点: 三角形全等之截长补短
-
3.(本小题25分)
已知,如图,在五边形ABCDE中,AB=AE,AD平分∠CDE,∠BAE=2∠CAD,
求证:BC+DE=CD.
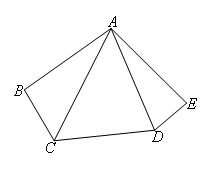
(截长法)证明:如图,
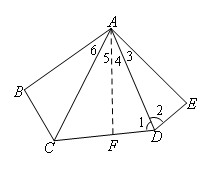
∵AD平分∠CDE
∴∠1=∠2
在△AFD和△AED中
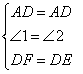
∴△AFD≌△AED(SAS)
∴
在△ABC和△AFC中
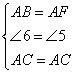
∴△ABC≌△AFC(SAS)
∴BC=CF
∴BC+DE=CF+DF
=CD
请你仔细观察下列序号所代表的内容:
①在CD上截取CF=CB,连接AF;②在DC上截取DF=DE,连接AF;
③在DC上截取DF=DE;④AE=AF;⑤AF=AE,∠4=∠3;⑥∠4=∠3;
⑦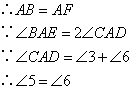 ;⑧
;⑧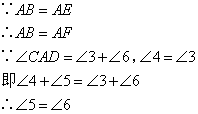 ;⑨
;⑨ .
.
以上空缺处依次所填最恰当的是( )
核心考点: 三角形全等之截长补短




 ;⑦
;⑦ ;
; .
.

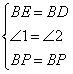
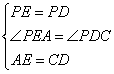
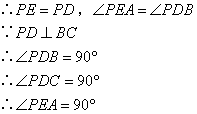 ;⑦
;⑦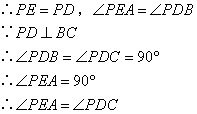 .
.

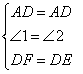
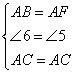
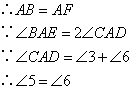 ;⑧
;⑧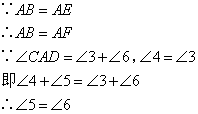 ;⑨
;⑨ .
.



 ;
; ;⑦
;⑦ ;
; ;⑨
;⑨ .
.