三角形全等之类比探究(照搬字母、辅助线二)(北师版)
满分100分 答题时间30分钟
已经有5位用户完成了练习
单选题(本大题共小题, 共分)
-
1.(本小题33分)
在四边形ABCD中,∠A=∠ABC=∠ADC=90°,∠ABD=45°,BC=CD,E为AB边上任意一点,过点E作EF⊥AB,交BD于点F,取DF的中点G,连接EG,CG.
(1)如图1,求证:EG⊥CG.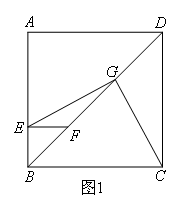
先在图上走通思路后再填写空格内容:
(1)如图,延长EG,交AD的延长线于点H,连接CE,CH.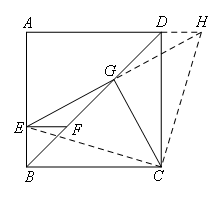
下面给出了证明的路线图: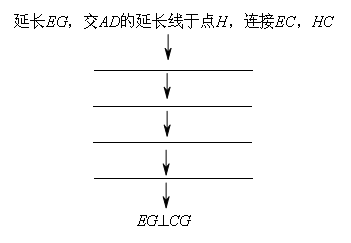
请你仔细观察下列序号所代表的内容:
①△EFG≌△HDG(ASA);②△CBE≌△CDH(SAS);③△CBE≌△CDH(AAS);
④EF=DH,EG=HG;⑤EF=DH,∠AFG=∠HDG;⑥EC=HC;⑦EC=HC,∠HCD=∠ECB.
以上横线处,依次所填最恰当的是( )
核心考点: 三角形全等之类比探究
-
3.(本小题34分)
(上接第1,2题)(3)在图1的基础上,将△BEF绕点B旋转,使点E在AB的延长线上,其他条件不变,如图3,求证:EG⊥CG.
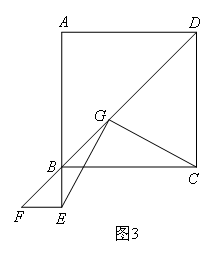
证明:如图, (叙述辅助线).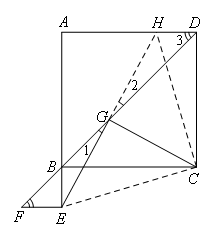
由图1可知,△BEF是等腰直角三角形,∠BEF=90°,EB=EF
∵∠A=90°
∴∠A=∠BEF
∴EF∥AB
∴∠F=∠3
∵点G是FD的中点
∴FG=DG
在△EFG和△HDG中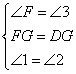
∴△EFG≌△HDG( )
∴
∵BE=EF
∴BE=DH
∵∠ABC=∠ADC=90°
∴∠EBC=∠HDC=90°
∴CE=CH
即△ECH为等腰三角形
∵EG=HG
∴EG⊥CG
请你仔细观察下列序号所代表的内容:
①延长EG,交AD于点H,连接CE,CH;②延长EG,交CD的延长线于点H,连接CE;③延长EG到H,
交AD于点H,使HG=EG,连接CE,CH;④AAS;⑤ASA;⑥EG=HG,EF=DH;⑦EG=HG,∠F=∠3;
⑧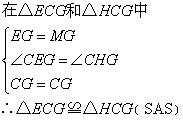 ;⑨
;⑨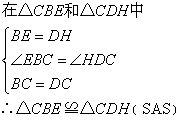 .
.
以上空缺处依次所填最恰当的是( )
核心考点: 三角形全等之类比探究







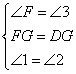
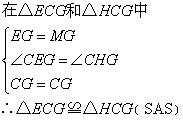 ;⑨
;⑨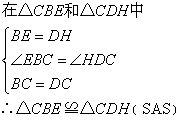 .
.