河南中考选填限时练(四)
满分45分 答题时间20分钟
已经有76位用户完成了练习
单选题(本大题共小题, 共分)
-
9.(本小题3分)
已知∠AOB=45°,求作∠AOP=22.5°,作法:
(1)以O为圆心,任意长为半径画弧分别交OA,OB于点N,M;
(2)分别以N,M为圆心,以OM长为半径在角的内部画弧交于点P;
(3)作射线OP,则OP为∠AOB的平分线,可得∠AOP=22.5°.
根据以上作法,某同学有以下3种证明思路:
①可证明△OPN≌△OPM,得∠POA=∠POB,可得;
②可证明四边形OMPN为菱形,OP,MN互相垂直平分,得∠POA=∠POB,可得;
③可证明△PMN为等边三角形,OP,MN互相垂直平分,从而得∠POA=∠POB,可得.
你认为该同学以上3种证明思路中,正确的有( )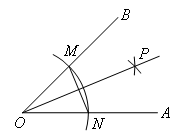
核心考点: 尺规作图