三角形的外角过程训练（综合一）（人教版）-八年级试卷-众享学科测评

三角形的外角过程训练（综合一）（人教版）

满分100分答题时间30分钟

已经有40位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题16分) 已知：如图，在△ABC中，D是AB边上一点，E是AC边上一点，DE的延长线交BC的延长线于点F．若∠ACB=50°，∠EFC=30°，∠ADE=80°．求∠A的度数． 解：如图， ∵∠ADE是△BDF的一个外角（外角的定义） ∴∠ADE=∠B+∠EFC（三角形的一个外角等于和它不相邻的两个内角的和） ∵∠EFC=30°，∠ADE=80°（已知） ∴∠B=∠ADE-∠EFC =80°-30° =50°（等式的性质） ∵∠ACB=50°（已知） ∴ 横线处应填写的过程最恰当的是( )

2.(本小题16分) 已知：如图，AB∥EF，∠E=∠CAE，∠DAB=65°． 求∠ACF的度数． 解：如图， ∵∠ACF是△ACE的一个外角（外角的定义） ∴∠ACF=∠E+∠CAE（三角形的一个外角等于和它不相邻的两个内角的和） ∵∠E=∠CAE（已知） ∴∠ACF=∠E+∠E =2∠E =2×65° =130°（等量代换） 横线处应填写的过程最恰当的是( )

3.(本小题16分) 如图，在△ABC中，D是AB边上一点，E是AC边上一点，BE，CD相交于点F． 若∠A=60°，∠ACD=35°，∠BFC=115°，求∠ABE的度数． 解：如图， ∵∠BFC是△EFC的一个外角（外角的定义） ∴∠BFC=∠FEC+∠ACD（三角形的一个外角等于和它不相邻的两个内角的和） ∵∠FEC是△ABE的一个外角（外角的定义） ∴∠FEC=∠A+∠ABE（三角形的一个外角等于和它不相邻的两个内角的和） ∵∠A=60°（已知） ∴∠ABE=∠FEC-∠A =80°-60° =20°（等式的性质） 横线处应填写的过程最恰当的是( )

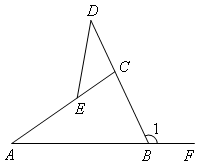
4.(本小题16分) 已知：如图，在△ABC中，∠1是它的一个外角，E是AC边上一点，延长BC到D， 连接DE．若∠AED=135°，∠A=∠D=35°，求∠1的度数． 解：如图， ∵∠AED是△DEC的一个外角（外角的定义） ∴∠AED=∠D+∠DCE（三角形的一个外角等于和它不相邻的两个内角的和） ∵∠AED=135°，∠D=35°（已知） ∴∠DCE=∠AED-∠D =135°-35° =100°（等式的性质） ∴∠ACB=180°-∠DCE =180°-100° =80° （平角的定义） ∵∠A=35°（已知） ∴∠1=35°+80° =115°（等量代换） 横线处应填写的过程最恰当的是( )

5.(本小题16分) 已知：如图，BC⊥DE，垂足为F，∠A=27°，∠D=20°，求∠B的度数． 解：如图， ∵∠A=27°，∠D=20°（已知） ∴∠BED=27°+20° =47°（等量代换） ∵BC⊥DE（已知） ∴∠EFB=90°（垂直的定义） ∴∠B+∠BED=90°（直角三角形两锐角互余） ∴∠B=90°-∠BED =90°-47° =43°（等式的性质） 横线处应填写的过程最恰当的是( )

6.(本小题20分) 如图所示，AB∥CD，E，G分别是直线AB，CD上的点，EF交CD于点H，连接FG． 若∠F=20°，∠HGF=40°，求∠AEH的度数． 解：如图， ∵AB∥CD（已知） ∴∠AEH=∠EHG（两直线平行，内错角相等） ∴∠AEH=60°（等量代换） 横线处应填写的过程最恰当的是( )