全等三角形的判定综合复习(二)(人教版)
满分100分 答题时间30分钟
已经有23位用户完成了练习
单选题(本大题共小题, 共分)
-
12.(本小题12分)
如图,四边形ABCD为正方形,∠ABC=∠BCD=90°,AB=BC=CD=AD,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,∠ABF=∠CBF,连接CF,交DE于点G.判断CF与ED的位置关系,并说明理由.
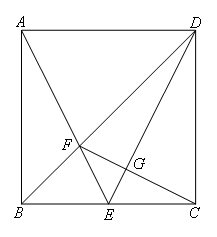
解:垂直.理由如下:
在△ABF与△CBF中
∴
∴∠BAF=∠BCF
在Rt△ABE和Rt△DCE中
∴
∴∠BAE=∠CDE
∴∠BCF=∠CDE
∵∠CDE+∠DEC=90°
∴∠BCF+∠DEC=90°
∴DE⊥CF
请你仔细观察下列序号所代表的内容:
①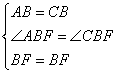 ,②
,②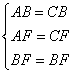 ,③
,③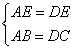 ,④
,④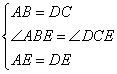 ,
,
⑤Rt△ABE≌Rt△DCE(HL),⑥△ABE≌△DCE(SAS),⑦△ABF≌△CBF(SAS),⑧△ABF≌△CBF(SSS).
以上空缺处依次填写正确的是( )
核心考点: 全等三角形的判定与性质 全等三角形证明过程训练













 ;②
;② ;
;
 ;
; ;④
;④ ;
;
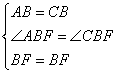 ,②
,②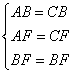 ,③
,③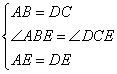 ,
,