综合复习——类比探究(人教版)
满分100分 答题时间30分钟
已经有11位用户完成了练习
单选题(本大题共小题, 共分)
-
3.(本小题14分)
如图1,在正方形ABCD和正方形CGEF(CG
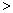 BC)中,点B,C,G在同一直线上,点M是AE的中点.
BC)中,点B,C,G在同一直线上,点M是AE的中点.
(1)探究线段MD,MF的位置关系,并证明.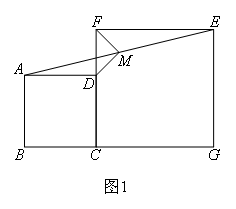
解题思路:(1)小明猜测MD⊥MF,看到图1中M是AE的中点,并且AD∥EF,考虑延长DM交EF于点H,如下图,先利用全等三角形的判定定理ASA,证明 ,由全等的性质可以得到 ,所以CD=EH,进而可以得到FD=FH,在等腰△DFH中,由等腰三角形三线合一可以得到 ,从而证明结论.
以上横线处,依次所填正确的是( )
①△ADM≌△EHM;②△FDM≌△FHM;③DM=HM,AD=HE;④FD=FH;⑤MF⊥DH;⑥FM平分∠DFH.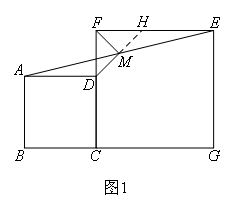
核心考点: 类比探究问题
-
4.(本小题14分)
(上接第3题)(2)将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线
CE恰好与正方形ABCD的边BC在同一条直线上,如图2,其他条件不变,(1)中得到的结论是否发生改变,写出猜想并加以证明.
解题思路:(2)小明类比第(1)问的解法,看到图2中M是AE的中点,并且AD∥EC,考虑延长DM交BE于点H,连接FD,FH,如下图,先证明 ,由全等的性质可以得到 .因为CD=AD,所以CD=HE,结合题目中的条件FC=FE,∠DCF=∠FEH=45°,又可以利用判定定理 证得 ,得到FD=FH,在等腰
△DFH中,由等腰三角形三线合一,得到MF⊥DH,从而证明结论.
以上横线处,依次所填正确的是( )
①△ADM≌△EHM;②△DCF≌△HEF;③DM=HM,AD=HE;④FD=FH;⑤SSA;⑥ASA;⑦SAS.
核心考点: 类比探究问题











