八年级数学 全等三角形单元练习(一)(人教版)
满分120分 答题时间100分钟
已经有32位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
23.(本小题11分)
如图1,AB=4 cm,AC⊥AB,BD⊥AB,AC=BD=3 cm.点P在线段AB上以1 cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为ts.
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由.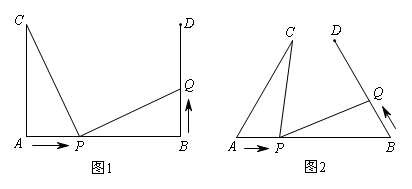
核心考点: 全等三角形的判定 动点























