九年级数学图形的相似单元练习（一）（华师版）-九年级试卷-众享学科测评

九年级数学图形的相似单元练习（一）（华师版）

满分120分答题时间100分钟

已经有75位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 已知，那么下列等式中，不一定正确的是( )

2.(本小题3分) 若一个多边形的各边长分别为2，3，4，5，6，另一个和它相似的多边形的最长边长为24，则另一个多边形的最短边长为( )

3.(本小题3分) 已知△ABC平移后得到△A₁B₁C₁，且A₁(-2，3)，B₁(-4，-1)，C₁(m，n)，C(m+5，n+3)，则A，B两点的坐标为( )

4.(本小题3分) 如图，已知AB∥CD∥EF，AD:AF=3:5，BE=12，那么CE的长等于( )

5.(本小题3分) 如图，利用标杆BE测量建筑物的高度．已知标杆BE高1.2 m，测得AB=1.6 m，BC=12.4 m，则建筑物CD的高是( )

6.(本小题3分) 如图，在△ABC中，点D，E分别在AC，AB上且DE∥BC，若S_△_ADE:S_△_BDE=2:3，则S_△_ADE:S_△_ACB=( )

7.(本小题3分) 如图，线段AB两个端点的坐标分别为A(2，2)，B(3，1)，以原点O为位似中心，在第一象限内将线段AB扩大为原来的2倍后得到线段CD，则端点C的坐标为( )

8.(本小题3分) 如图，△ABC中，∠ACB=90°，分别以AB，AC为边作正方形ABPQ，ACFH，BP交FH于点O．若BC=BF=2，则OP的长为( )

9.(本小题3分) 如图，BE，CF为△ABC的两条高，若AB=6，BC=5，EF=3，则AE的长为( )

10.(本小题3分) 在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为(1，0)，点D的坐标为 (0，2)，延长CB交x轴于点A₁，作第2个正方形A₁B₁C₁C；延长C₁B₁交x轴于点A₂，作第3个正方形A₂B₂C₂C₁……，按这样的规律进行下去，第2021个正方形的面积为( )

填空题(本大题共小题，共分)

11.(本小题3分) 在比例尺为1:4 000 000的地图上，两城市间的图上距离为3 cm，则这两城市间的实际距离为____km．

12.(本小题3分) 若线段a，b满足，则的值为____．

13.(本小题3分) 某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米，然后向正西方向飞行300千米，又测得该机场的位置位于监控中心的西100千米，北300千米的地方，若以监控中心为坐标原点，以正东、正北方向为x轴、y轴的正方向，请指出该飞机现在的位置____（用坐标表示）．

14.(本小题3分) 从三角形（非等腰三角形）一个顶点引出一条射线与对边相交，该顶点与该交点间的线段把这个三角形分割成两个小三角形，如果其中一个小三角形是等腰三角形，另一个与原三角形相似，那么我们把这条线段叫做这个三角形的完美分割线．如图，在△ABC中，DB=1，BC=2，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，则CD的长为____．

15.(本小题3分) 在中学数学中求一些图形面积时，经常用到“同底等高”“等底等高”等数学思想方法，我们称它为等积变换．如图，BD为□ABCD的对角线，M，N分别在AD，AB上，且，若S_△_DMC=3，则S_△_BNC+S_△_AMN=____．

解答题(本大题共小题，共分)

16.(本小题8分) 如图，已知AD为△ABC的角平分线，∠ADE=∠B． （1）求证：△ABD∽△ADE； （2）若AB=9，AE=4，求AD的长．

17.(本小题8分) 如图，在平面直角坐标系中，四边形OABC的顶点坐标分别是O(0，0)，A(3，0)，B(4，4)， C(-2，3)，将点O，A，B，C的横坐标、纵坐标都乘以-2． （1）画出以变化后的四个点为顶点的四边形； （2）由（1）得到的四边形与四边形OABC位似吗？如果位似，指出位似中心及与原图形的相似比．

18.(本小题9分) 如图，AD是直角三角形△ABC斜边上的高． （1）若AD=6cm，CD=12cm，求BD的长； （2）若AB=15cm，BC=25cm，求BD的长．

19.(本小题9分) 如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B． （1）在图中找出一对相似三角形，并说明理由； （2）若AB=8，AD=，AF=，求AE的长．

20.(本小题10分) 某校数学实践社团开展了一次“利用数学知识测量学校操场上旗杆高度”的实践活动，该校九年级学生积极参与．小红和小华决定利用下午课间的时间，用测量影长的方式求出旗杆高度．同一时刻测量站在旗杆旁边的小红（CD）和旗杆AB的影长时，发现旗杆的影子一部分落在地面上（BF），另一部分落在了距离旗杆24m的教学楼上（EF）．经测量，小红落在地面上的影长DG为2.4m，教学楼上的影长EF为2m．已知小红的身高是1.6m，请根据小红和小华的测量结果，求出旗杆AB的高度．

21.(本小题10分) （2021广东）在平面直角坐标系xOy中，一次函数y=kx+b（k＞0）的图象与x轴、y轴分别交于A，B两点，且与反比例函数图象的一个交点为P(1，m)． （1）求m的值； （2）若PA=2AB，求k的值．

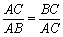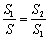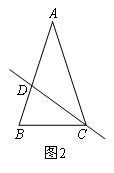
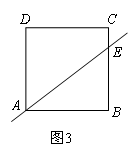
22.(本小题10分) 如图1，点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点．某教学兴趣小组在进行研究时，由“黄金分割点”联想到“黄金分割线”，类似的给出“黄金分割线”的定义：一直线将一个面积为S的图形分成两部分，这两部分的面积分别为S₁，S₂，如果，那么称这条直线为该图形的黄金分割线． （1）如图2，在ABC中，∠A=36°，AB=AC，∠C的平分线交AB于点D，请问直线CD是不是△ABC的黄金分割线，并证明你的结论； （2）如图3，在边长为1的正方形ABCD中，点E是边BC上一点，若直线AE是正方形ABCD的黄金分割线，求BE的长．

23.(本小题11分) （2019长春）教材呈现：下面是华师版九年级上册数学教材第78页的部分内容． 例2，如图，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证：． 证明：连接ED． 请根据教材提示，结合图1，写出完整的证明过程． 结论应用：在□ABCD中，对角线AC，BD交于点O，E为边BC的中点，AE，BD交于点F． （1）如图2，若□ABCD为正方形，且AB=6，则OF的长为； （2）如图3，连接DE交AC于点G，若四边形OFEG的面积为，则□ABCD的面积为．