九年级数学 旋转单元练习(二)(人教版)
满分120分 答题时间100分钟
已经有3位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
21.(本小题10分)
新知学习:求函数变换后的图象的解析式是数学学习的一个难点.可以通过下面的方法解决此类问题:先设点P(x,y)为所求函数图象上任意一点,求出点P变换前的对应点的坐标P′(x′,y′),把点P′的坐标代入原解析式,整理即可求出所求的解析式.
例如:求直线y=2x-3关于原点对称的直线的解析式.
解:设P(x,y)为所求直线上任意一点,则P关于原点对称的点P′(-x,-y)在直线y=2x-3上,代入得:
-y=2(-x)-3.整理得:y=2x+3即为所求.
利用上面的方法解决下列问题:
(1)求直线y=-3x+5关于原点对称的直线解析式;
(2)求将抛物线y=-x2+2x+3向下平移2个单位,再向左平移1个单位后的解析式;
(3)直接写出y=x2-2x-3关于x轴对称的抛物线的解析式.
核心考点: 二次函数 中心对称 平移 轴对称
-
23.(本小题11分)
(2021鄂尔多斯)旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.
(1)尝试解决:如图1,在等腰Rt△ABC中,∠BAC=90°,AB=AC,点M是BC上的一点,BM=1 cm,CM=2 cm,将△ABM绕点A旋转后得到△ACN,连接MN,则AM= cm;
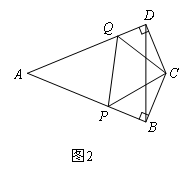
(2)类比探究:如图2,在“筝形”四边形ABCD中,AB=AD=a,CB=CD,AB⊥BC于点B,AD⊥CD于点D,点P,Q分别是AB,AD上的点,且∠PCB+∠QCD=∠PCQ,求△APQ的周长;(结果用a表示)
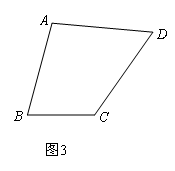
(3)拓展应用:如图3,已知四边形ABCD,AD=CD,∠ADC=60°,∠ABC=75°,AB=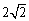 ,BC=2,求四边形ABCD的面积.
,BC=2,求四边形ABCD的面积.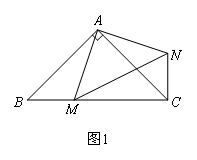
核心考点: 旋转 面积



























