九年级数学随机事件的概率单元练习（二）（华师版）-九年级试卷-众享学科测评

天天练

九年级数学随机事件的概率单元练习（二）（华师版）

满分120分答题时间100分钟

已经有0位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 一个布袋中装有9个白球，n个红球，从中任意取出一个红球的概率为，则n为( )

2.(本小题3分) 某商场利用摸奖开展促销活动，中奖率为，则下列说法正确的是( )

3.(本小题3分) 在综合实践活动中，小明、小亮、小颖、小静四位同学用投掷图钉的方法估计针尖朝上的概率，他们的实验次数分别为20次、50次、150次、200次，其中哪位同学的实验相对科学( )

4.(本小题3分) 在抛一枚均匀硬币的实验中，如果没有硬币，则下列实物可作替代实验的是( )

5.(本小题3分) 下列说法正确的是( )

6.(本小题3分) 如图1所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个长为8 m，宽为5 m的长方形，将不规则图案围起来，然后在适当位置随机朝长方形区域扔小球，并记录小球落在不规则图案上的次数（小球扔在界线上或长方形区域外不计入试验结果），他将若干次有效试验的结果绘制成了图2所示的折线统计图，由此可估计不规则图案的面积大约是( )

7.(本小题3分) 四张扑克牌分别是红桃A，黑桃A，方块A，梅花A，将它们的正面向下随机摆放在桌面上，从中任意抽出一张，则抽出的扑克牌的图案为红色的概率是( )

8.(本小题3分) 图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则这两个数的和是2的倍数或是3的倍数的概率等于( )

9.(本小题3分) 在某校春季运动会4×100 m接力赛中，甲、乙同学都是第一棒，甲、乙同学随机从4个赛道中抽取赛道，则甲、乙两名同学抽中的赛道之间间隔一个赛道的概率为( )

10.(本小题3分) （2021安徽）如图在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点A的概率是( )

填空题(本大题共小题，共分)

11.(本小题3分) 在一个不透明的布袋中装有红色、白色玻璃球共40个，除颜色外其他完全相同．小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在15%左右，则口袋中红色球可能有____个．

12.(本小题3分) 要在一个口袋中装入若干个大小、质量都完全相同的球，使得从袋中摸到一个红球的概率是，可以怎样放球____．

13.(本小题3分) 小明的书包里只放了A4大小的试卷共5张，其中语文3张，数学2张．若随机地从书包中抽出2张，抽出的试卷恰好都是数学试卷的概率是____．

14.(本小题3分) 从0，1，2，3，4这5个数中任选一个数作为m的值，则使不等方式组无实数解，且使得正比例函数y=(m-4)x中因变量y随自变量x的增大而减小的概率是____．

15.(本小题3分) 如图，在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点，任意三个格点组成的三角形面积如果不小于1，则称为“离心三角形”，而如果面积恰好等于1，则称为“环绕三角形”．A，B是网格图形中已知的两个格点，点C是另一格点，且满足△ABC是“离心三角形”，则△ABC是“环绕三角形”的概率是____．

解答题(本大题共小题，共分)

16.(本小题8分) 从同一副扑克牌中拿出黑桃2，3，4，5，背面朝上洗匀后摆在桌面上，从中随机抽取一张（不放回），再从剩下的3张中随机抽取第二张． （1）用树状图的方法，列出前后两次抽得的扑克牌上所标数字的所有可能情况； （2）计算抽得的两张扑克牌上数字之积为奇数的概率．

17.(本小题8分) 木盒里有红球和白球，共4个，每个球除了颜色外其他都相同．从盒子里先摸出一个球，放回去摇匀后，再摸出一个球，继续放回去摇匀后，再摸第3次、第4次… （1）甲同学摸球10次，都没有摸到红球，于是他就判断“摸到红球”是“不可能事件”．他的判断正确吗？ （2）如果盒子里有3个红球、1个白球，乙同学按照摸球的规则，摸球2次，那么摸到1个红球和1个白球的概率是多少？（用树状图或列表法求解）

18.(本小题9分) （2021常州）在3张相同的小纸条上，分别写上条件：①四边形ABCD是菱形；②四边形ABCD有一个内角是直角；③四边形ABCD的对角线相等．将这3张小纸条做成3支签，放在一个不透明的盒子中． （1）搅匀后从中任意抽出1支签，抽到条件①的概率是； （2）搅匀后先从中任意抽出1支签（不放回），再从余下的2支签中任意抽出1支签．四边形ABCD同时满足抽到的2张小纸条上的条件，求四边形ABCD一定是正方形的概率．

19.(本小题9分) （2021福建）“田忌赛马”的故事闪烁着我国古代先贤的智慧光芒．该故事的大意是：齐王有上、中、下三匹马A₁，B₁，C₁，田忌也有上、中、下三匹马A₂，B₂，C₂，且这六匹马在比赛中的胜负可用不等式表示如下：A₁＞A₂＞B₁＞B₂＞C₁＞C₂（注：A＞B表示A马与B马比赛，A马获胜）．一天，齐王找田忌赛马，约定：每匹马都出场比赛一局，共赛三局，胜两局者获得整场比赛的胜利．面对劣势，田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马，并采用孙膑的策略：分别用下马、上马、中马与齐王的上马、中马、下马比赛，即借助对阵（C₂A₁，A₂B₁，B₂C₁）获得了整场比赛的胜利，创造了以弱胜强的经典案例． 假设齐王事先不打探田忌的“出马”情况，试回答以下问题： （1）如果田忌事先只打探到齐王首局将出“上马”，他首局应出哪种马才可能获得整场比赛的胜利？并求其获胜的概率； （2）如果田忌事先无法打探到齐王各局的“出马”情况，他是否必败无疑？若是，请说明理由；若不是，请列出田忌获得整场比赛胜利的所有对阵情况，并求其获胜的概率．

20.(本小题10分) 某商场设立了一个可以自由转动的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品． 下表是活动进行中的一组统计数据： （1）计算并完成表格： （2）请估计，当n很大时，频率将会接近（精确到0.1）． （3）假如你去转动该转盘一次，你获得铅笔的概率约是，理由是．

21.(本小题10分) 小明对A，B，C，D四个中小型超市的女工人数进行了统计，并绘制了下面的统计图表，已知A超市有女工20人． （1）A超市共有员工多少人？B超市有女工多少人？ （2）若从这些女工中随机选出一个，求正好是C超市的概率； （3）现在D超市又招进男、女员工各1人，D超市女工占比还是75%吗？甲同学认为是，乙同学认为不是，你认为谁说的对，并说明理由．

22.(本小题10分) 在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色后，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据： （1）若从盒子里随机摸出一球，则摸到白球的概率约为；（精确到0.1） （2）估算盒子里约有白球个； （3）若向盒子里再放入x个除颜色以外其他完全相同的球，这x个球中白球只有1个．然后每次将球搅拌均匀后，任意摸出一个球记下颜色后再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在50%，请你推测x可能是多少？

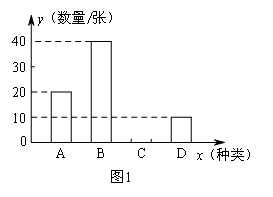
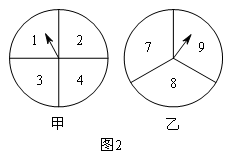
23.(本小题11分) 假期，某市教育局组织部分教师分别到A，B，C，D四个地方进行新课程培训，教育局按定额购买了前往四地的车票，图1是未制作完成的车票种类和数量的条形统计图． 请根据统计图回答下列问题： （1）若去C地的车票占全部车票的30%，则去C地的车票有张，补全条形统计图； （2）若教育局采用随机抽签的方式分发车票，每人一张（所有车票的情况、大小、质地完全相同且充分洗匀），那么于老师抽到去B地的车票的概率是多少？ （3）若有一张去A地的车票，张老师和李老师都想要，他们决定采取转转盘的方式来确定．其中甲转盘被分成四等份且分别标有数字1，2，3，4，乙转盘被分成三等份且分别标有数字7，8，9，如图2所示． 具体规定是：同时转动两个转盘，当指针指向的两个数字之和是偶数时，票给李老师，否则票给张老师（指针指在线上重转）．试用列表法或画树状图的方法分析这个规定对双方是否公平．

九年级数学 随机事件的概率单元练习（二）（华师版）

单选题(本大题共小题， 共分)

填空题(本大题共小题， 共分)

解答题(本大题共小题， 共分)

九年级数学随机事件的概率单元练习（二）（华师版）

单选题(本大题共小题，共分)

填空题(本大题共小题，共分)

解答题(本大题共小题，共分)