九年级数学 圆单元练习(二)(人教版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
18.(本小题9分)
材料阅读
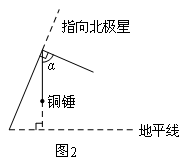
地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1中的⊙O).人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角α的大小是变化的.
实际应用
观测点A在图1所示的⊙O上,现在利用这个工具尺在点A处测得α为31°,在点A所在子午线往北的另一个观测点B,用同样的工具尺测得α为67°.PQ是⊙O的直径,PQ⊥ON.
(1)求∠POB的度数;
(2)已知OP=6 400 km,求这两个观测点之间的距离即⊙O上弧AB的长.(π取3.1)
(AG,BH所在直线与直线ON平行,在观测点处的地平线就是过该点的⊙O的切线哦!)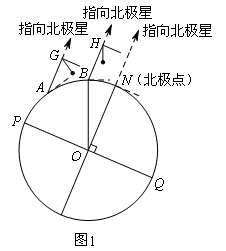
核心考点: 应用题 直线和圆的位置关系 弧长























