九年级数学 投影与视图单元练习(二)(北师版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
23.(本小题11分)
学习投影后,小明、小颖利用灯光下自己的影子的长度来测量一路灯的高度,并探究影子的长度的变化规律.如图所示,在同一时刻,身高为1.6m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置点G.
(2)求路灯灯泡的垂直高度GH.
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH的中点B1处时,其影子B1C1的长为 ;当小明继续走剩下路程的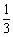 到点B2处时,其影子B2C2的长为 ;当小明继续走剩下路程的
到点B2处时,其影子B2C2的长为 ;当小明继续走剩下路程的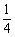 到点B3处时,其影子B3C3的长为 ;…按此规律继续走下去,当小明走剩下路程的
到点B3处时,其影子B3C3的长为 ;…按此规律继续走下去,当小明走剩下路程的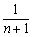 到点Bn处时,其影子BnCn的长为 m.(直接用含n的代数式表示)
到点Bn处时,其影子BnCn的长为 m.(直接用含n的代数式表示)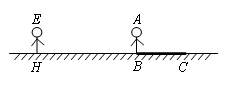
核心考点: 中心投影

























