九年级数学概率初步单元练习（一）（人教版）-九年级试卷-众享学科测评

九年级数学概率初步单元练习（一）（人教版）

满分120分答题时间100分钟

已经有0位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 随意转动如图所示的转盘，指针所落位置可能性最小的是( )

2.(本小题3分) （2021贺州）下列事件中属于必然事件的是( )

3.(本小题3分) （2021怀化）“成语”是中华文化的瑰宝，是中华文化的微缩景观．下列成语：①“水中捞月”，②“守株待兔”，③“百步穿杨”，④“瓮中捉鳖”描述的事件是不可能事件的是( )

4.(本小题3分) 小刚掷一枚均匀的硬币，一连9次都掷出正面朝上，当他第十次掷硬币时，出现正面朝上的概率是( )

5.(本小题3分) 甲、乙两人做掷骰子游戏，规定：一人掷一次，若两人所掷骰子的点数和大于6，则甲胜；反之，乙胜．则甲、乙两人中( )

6.(本小题3分) 用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，那么可配成紫色的概率是( )

7.(本小题3分) 在边长为1的小正方形组成的网格中，有如图所示的A，B两点，在格点上任意放置点C，恰好能得到面积为1的△ABC的概率为( )

8.(本小题3分) 关于频率与概率有下列几种说法，正确的是( ) ①“明天下雨的概率是90%”表示明天下雨的可能性很大； ②“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上； ③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖； ④“抛一枚硬币正面朝上的概率为”表示随着抛掷次数的增加， “抛出正面朝上”这一事件发生的频率稳定在附近．

9.(本小题3分) 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在0.15和0.45，则口袋中白色球的个数可能是( )

10.(本小题3分) 在平面直角坐标系中，作△OAB，其中三个顶点分别是O(0，0)，B(1，1)，A(x，y)（-2≤x≤2，-2≤y≤2，x，y均为整数），则所作△OAB为直角三角形的概率是( )

填空题(本大题共小题，共分)

11.(本小题3分) 小明在做掷一枚普通的正方体骰子实验，请写出这个实验中一个可能发生的事件：____．

12.(本小题3分) 如图，创意广场上铺设了一种新颖的石子图案，它由五个过同一点且半径不同的圆组成，其中阴影部分铺黑色石子，其余部分铺白色石子．小鹏在规定地点随意向图案内投掷小球，小球都能落在图案内，经过多次试验，发现落在一、三、五环（阴影）内的概率分别是0.04，0.2，0.36，如果最大圆的半径是1，则黑色石子区域的总面积为____．

13.(本小题3分) （2021通辽）如图所示，电路连接完好，且各元件工作正常．随机闭合开关S₁，S₂，S₃中的两个，能让两个小灯泡同时发光的概率是____．

14.(本小题3分) （2021嘉兴、舟山）看了《田忌赛马》故事后，小杨用数学模型来分析：齐王与田忌的上中下三个等级的三匹马记分如表，每匹马只赛一场，两数相比，大数为胜，三场两胜则赢．已知齐王的三匹马出场顺序为10，8，6．若田忌的三匹马随机出场，则田忌能赢得比赛的概率为____．

15.(本小题3分) （2021呼和浩特）动物学家通过大量的调查，估计某种动物活到20岁的概率为0.8，活到25岁的概率为0.5，据此若设刚出生的这种动物共有a只，则20年后存活的有____只，现年20岁的这种动物活到25岁的概率是____．

解答题(本大题共小题，共分)

16.(本小题8分) 一个不透明的布袋中有4个红球、5个白球、11个黄球，它们除颜色外都相同． （1）求从袋中摸出一个球是红球的概率； （2）现从袋中取走若干个黄球，并放入相同数量的红球，搅拌均匀后，要使从袋中摸出一个球是红球的概率不小于，问至少需取走多少个黄球？

17.(本小题9分) （2021河北）某博物馆展厅的俯视示意图如图1所示．嘉淇进入展厅后开始自由参观，每走到一个十字道口，她自己可能直行，也可能向左转或向右转，且这三种可能性均相同． （1）求嘉淇走到十字道口A向北走的概率； （2）补全图2的树状图，并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大．

18.(本小题9分) 如图，一个转盘被平均分成12份，每份上写上不同的数字，游戏方法：先猜数后转动转盘，若指针指向的数字与所猜的数一致，则猜数者获胜．现提供三种猜数方法： ①猜是“奇数”，或是“偶数”； ②猜是“大于10的数”，或是“不大于10的数”； ③猜是“3的倍数”，或是“不是3的倍数”； 如果你是猜数者，你愿意选择哪一种猜数方法？怎样猜？并说明理由．

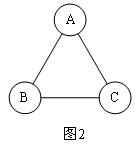
19.(本小题9分) 如图1，一枚质地均匀的正四面体骰子，它有四个面，并分别标有1，2，3，4四个数字；如图2，等边三角形ABC的三个顶点处各有一个圆圈．丫丫和甲甲想玩跳圈游戏，游戏的规则为：游戏者从圈A起跳，每投掷一次骰子，骰子着地的一面点数是几，就沿着三角形的边逆时针方向连续跳跃几个边长．如：若第一次掷得点数为2，就逆时针连续跳2个边长，落到C；若第二次掷得点数为4，就从圈C继续逆时针连续跳4个边长，落到圈A． （1）丫丫随机掷一次骰子，她跳跃后落回到圈A的概率为； （2）丫丫和甲甲一起玩跳圈游戏：ㄚ丫随机投掷一次骰子，甲甲随机投掷两次骰子，都以最终落回到圈A为胜者．这个游戏规则公平吗？请说明理由．

20.(本小题9分) 锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用（使用“求助”一次可以让主持人去掉其中一题的一个错误选项）． （1）如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是． （2）如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是． （3）如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．

21.(本小题10分) （2021赤峰）某学校九年级有12个班，每班50名学生，为了调查该校九年级学生平均每天的睡眠时间，准备从12个班里抽取50名学生作为一个样本进行分析，并规定如下：设每个学生平均每天的睡眠时间为t（单位，小时），将收集到的学生平均每天睡眠时间按t≤6，6<t<8，t≥8分为三类进行分析． （1）下列抽取方法具有代表性的是( ) A．随机抽取一个班的学生B．从12个班中，随机抽取50名学生 C．随机抽取50名男生D．随机抽取50名女生 （2）由上述具有代表性的抽取方法抽取50名学生，平均每天的睡眠时间数据如下表： ①这组数据的众数和中位数分别是，； ②估计九年级学生平均每天睡眠时间t≥8的人数大约为多少； （3）从样本中学生平均每天睡眠时间t≤6的4个学生里，随机抽取2人，画树状图或列表，求抽得2人平均每天睡眠时间都是6小时的概率．

22.(本小题10分) “2018年西安女子半程马拉松”的赛事有两项： A．“女子半程马拉松”； B．“5公里女子健康跑”． 小明对部分参赛选手作了如下调查： （1）计算表中a，b的值； （2）在图中，画出参赛选手参加“5公里女子健康跑”的频率的折线统计图； （3）从参赛选手中任选一人，估计该参赛选手参加“5公里女子健康跑”的概率（精确到0.1）．

23.(本小题11分) 有甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数0，1，2；乙袋中装有3个完全相同的小球，分别标有数-1，-2，0．现从甲袋中随机抽取一个小球，记录标有的数为x，再从乙袋中随机抽取一个小球，记录标有的数为y，确定点M的坐标为(x，y)． （1）用画树状图法或列表法列举点M的所有可能的坐标； （2）求点M(x，y)在函数y=-x+1的图象上的概率； （3）在平面直角坐标系xOy中，⊙O的半径是2，求过点M(x，y)能作⊙O的切线的概率．