九年级数学上学期阶段综合练习(一)(前4章)(人教版)
满分120分 答题时间100分钟
已经有7位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
21.(本小题10分)
某地有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1 000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售.
(1)设x天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额为P元,试写出P与x之间的函数关系式;
(3)李经理将这批野生菌存放多少天后出售可获得最大利润W,最大利润为多少元?(利润=销售总额-收购成本-各种费用)
核心考点: 二次函数应用题
-
22.(本小题10分)
在△ABC中,AC=BC,CD是AB边上的高.
问题发现:
(1)如图1,若∠ACB=90°,点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转90°,得到线段CF,连接BF,我们会发现CD,BE,BF之间的数量关系是CD=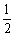 (BE+BF),请你证明这个结论;
(BE+BF),请你证明这个结论;
提出猜想:
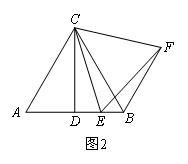
(2)如图2,若∠ACB=60°,点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转60°,得到线段CF,连接BF,猜想线段CD,BE,BF之间的数量关系是 ;
拓广探索:
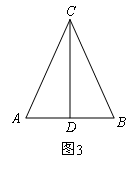
(3)若∠ACB=α,CD=k·AB(k为常数),点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转α,得到线段CF,连接BF.请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答.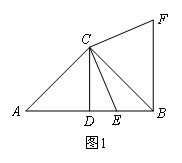
核心考点: 类比探究 旋转















