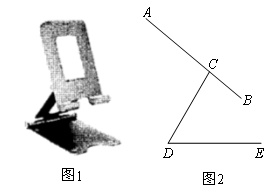九年级数学上学期阶段综合练习(一)(前4章)(华师版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
20.(本小题9分)
如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.量得托板长AB=120mm,支撑板长CD=80mm,底座长DE=90mm.托板AB固定在支撑板顶端点C处,且CB=40mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位)
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,sin26.6°≈0.448,cos26.6°≈0.894,tan26.6°≈0.500, ≈1.732)
≈1.732)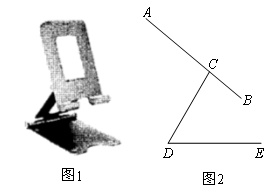
核心考点: 锐角三角函数的应用