九年级数学上学期阶段综合练习（二）（九上全部）（华师版）-九年级试卷-众享学科测评

九年级数学上学期阶段综合练习（二）（九上全部）（华师版）

满分120分答题时间100分钟

已经有0位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 若代数式有意义，则x的取值范围是( )

2.(本小题3分) 一元二次方程x²-3x-2=0的两根为x₁，x₂，则下列结论正确的是( )

3.(本小题3分) 关于随机事件A，下列叙述不正确的是( )

4.(本小题3分) 下面计算正确的是( )

5.(本小题3分) 如图，在平面直角坐标系中，已知A(-5，0)，B(5，0)，C(3，6)，则△ABC重心的坐标是( )

6.(本小题3分) 在一个不透明的袋子中装有除颜色外其余均相同的m个小球，其中5个黑球，从袋中随机摸出一球，记下其颜色，这称为依次摸球试验，之后把它放回袋中，搅匀后，再继续摸出一球．以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表： 根据列表，可以估计出m的值是( )

7.(本小题3分) 如图，在矩形ABCD中，AB=2，BC=，E是BC的中点，将△ABE沿直线AE翻折，点B落在点F处，连接CF，则cos∠ECF的值为( )

8.(本小题3分) 已知关于x的一元二次方程(a-1)x²-2x+1=0有两个不相等的实数根，则a的取值范围是( )

9.(本小题3分) 如图1，AB=5，射线AM∥BN，点C在射线BN上，将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，点P，Q分别在射线AM，BN上，PQ∥AB．设AP=x，QD=y．若y关于x的函数图象（如图2）经过点E(9，2)，则cosB的值等于( )

10.(本小题3分) 如图，在矩形ABCD中，点E为AD上一点，且AB=8，AE=3，BC=4，点P为AB上一动点，连接PC，PE，若△PAE与△PBC是相似三角形，则满足条件的点P有( )个．

填空题(本大题共小题，共分)

11.(本小题3分) 若最简二次根式与是同类二次根式，则a=____．

12.(本小题3分) 某公司2月份的利润为160万元，4月份的利润为250万元，若设平均每月的增长率为x，则根据题意可得方程为____．

13.(本小题3分) 大数据分析技术为打赢疫情防控阻击战发挥了重要作用．如图是小明同学的健康码（绿码）示意图，用黑白打印机打印于边长为2 cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.6左右，据此可以估计黑色部分的总面积约为____cm²．

14.(本小题3分) 如图，在四边形ABCD中，AC与BD相交于点O，∠ABC=∠DAC=90°，tan∠ACB=，，则____．

15.(本小题3分) 如图，在矩形ABCD中，AB=6，BC=8，对角线AC，BD相交于点O，点P为边AD上一动点，连接OP，以OP为折痕，将△AOP折叠，点A的对应点为点E，线段PE与OD相交于点F．若△PDF为直角三角形，则DP的长为____．

解答题(本大题共小题，共分)

16.(本小题8分) （1）解方程：2x²-5x+3=0； （2）在一个边长为cm的正方形的内部挖去一个长为cm，宽为cm的矩形，求剩余部分图形的面积．

17.(本小题9分) 如图，在矩形ABCD中，已知AD＞AB．在边AD上取一点E，连接CE，过点E作EF⊥CE，与边AB的延长线交于点F． （1）求证：△AEF∽△DCE； （2）若AB=4，AE=6，AD=14，求线段AF的长．

18.(本小题9分) 在“植树节”期间，小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动，规则如下：在两个盒子内分别装入标有数字1，2，3，4的四个和标有数字1，2，3的三个完全相同的小球，分别从两个盒子中各摸出一个球，如果所摸出的球上的数字之和小于5，那么小王去，否则就是小李去． （1）用树状图或列表法求出小王去的概率； （2）小李说：“这种规则不公平”，你认同他的说法吗？请说明理由．

19.(本小题9分) 某商店准备进一批季节性小家电，每个进价为40元，经市场预测，销售定价为50元，可售出400个；定价每增加1元，销售量将减少10个． 设每个定价增加x元． （1）写出售出一个可获得的利润是多少元（用含x的代数式表示）？ （2）商店若准备获得利润6 000元，并且使进货量较少，则每个定价为多少元？应进货多少个？

20.(本小题9分) 脱贫攻坚工作让老百姓过上了幸福的生活．如图1是政府给贫困户新建的房屋，如图2是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高AB所在的直线，为了测量房屋的高度，在地面上C点测得屋顶A的仰角为35°，此时地面上C点、屋檐上E点、屋顶上A点三点恰好共线，继续向房屋方向走8 m到达点D时，又测得屋檐E点的仰角为60°，房屋的顶层横梁EF=12 m，EF∥CB，AB交EF于点G（点C，D，B在同一水平线上）．（参考数据：sin35°≈0.6，cos35°≈0.8，tan35°≈0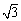.7，≈1.7） （1）求屋顶到横梁的距离AG； （2）求房屋的高AB（结果精确到1 m）．

21.(本小题10分) 如图，在△ABC中，∠ACB=90°，AC=6，BC=8，动点E从点A出发沿着线段AB向终点B运动，速度为每秒3个单位长度，过点E作EF⊥AB交直线AC于点F，连接CE．设点E的运动时间为t秒． （1）当点F在线段AC上（不含端点）时， ①求证：△ABC∽△AFE； ②当t为何值时，△CEF的面积为1.2； （2）在运动过程中，是否存在某时刻t，使△CEF为等腰三角形？若存在，求出t的值；若不存在，请说明理由．

22.(本小题10分) 如图1，△ABC与△CDE是等腰直角三角形，直角边AC，CD在同一条直线上，点M，N分别是斜边AB，DE的中点，点P为AD的中点，连接AE，BD． （1）猜想PM与PN的数量关系及位置关系，请直接写出结论； （2）现将图1中的△CDE绕着点C顺时针旋转α（0°<α<90°），得到图2，AE与MP，BD分别交于点G，H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由； （3）若图2中的等腰直角三角形变成直角三角形，使BC=kAC，CD=kCE，如图3，写出PM与PN的数量关系，并加以证明．

23.(本小题11分) Rt△ABC在直角坐标系内的位置如图所示，反比例函数（k≠0）在第一象限内的图象与BC边交于点D(4，m)，与AB边交于点E(2，n)，△BDE的面积为2． （1）求m与n的数量关系； （2）当时，求反比例函数的解析式和直线AB的解析式； （3）设P是线段AB边上的点，在（2）的条件下，是否存在点P，使以B，C，P为顶点的三角形与△EDB相似？若存在，求出此时点P的坐标；若不存在，请说明理由．