八年级数学 勾股定理单元练习(一)(华师版)
满分120分 答题时间100分钟
已经有1位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
23.(本小题12分)
(2020随州)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理.(以下图形均满足证明勾股定理所需的条件)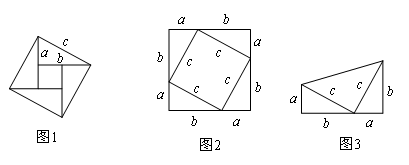
(2)①如图4,5,6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有 个;
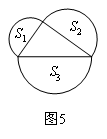
②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案的面积分别为S1,S2,直角三角形的面积为S3,请判断S1,S2,S3的关系并证明.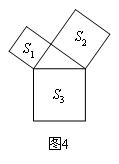


核心考点: 勾股定理的证明
























