九年级数学 二次函数单元练习(二)(华师版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
21.(本小题10分)
(2021荆门)某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,如表仅列出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应值数据.
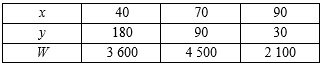
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;
(3)因疫情期间,该商品进价提高了m(元/件)(m>0),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系.若周销售最大利润是4 050元,求m的值.
核心考点: 二次函数应用题
-
23.(本小题11分)
(2021广安)如图,在平面直角坐标系中,抛物线y=-x2+bx+c的图象与坐标轴相交于A,B,C三点,其中点A的坐标为(3,0),点B的坐标为(-1,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒
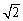 个单位长度的速度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度的速度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
个单位长度的速度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度的速度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
(1)求b,c的值.
(2)在P,Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?
(3)在线段AC上方的抛物线上是否存在点M,使△MPQ是以点P为直角顶点的等腰直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.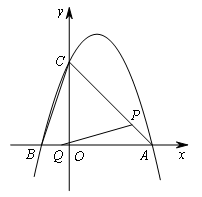
核心考点: 存在性问题 二次函数与几何综合 函数最值













