九年级数学 圆单元练习(一)(华师版)
满分120分 答题时间69分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
21.(本小题10分)
(2020鄂尔多斯)我们知道,顶点坐标为(h,k)的抛物线的解析式为y=a(x-h)2+k(a≠0).今后我们还会学到,圆心坐标为(a,b),半径为r的圆的方程(x-a)2+(y-b)2=r2,如:圆心为点P(-2,1),半径为3的圆的方程为(x+2)2+(y-1)2=9.
(1)以点M(-3,-1)为圆心,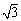 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)如图,以点B(-3,0)为圆心的圆与y轴相切于原点,点C是⊙B上一点,连接OC,作BD⊥OC,垂足为点D,延长BD交y轴于点E,已知sin∠AOC=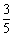 .
.
①连接EC,求证:EC是⊙B的切线;
②在BE上是否存在一点Q,使QB=QC=QE=QO?若存在,求点Q的坐标,并写出以点Q为圆心,以QB为半径的⊙Q的方程;若不存在,请说明理由.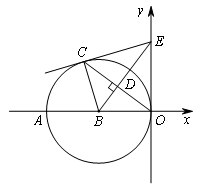
核心考点: 新定义 切线的判定
























